15.12 Konstruktionsfunktionen 

In dieser Gruppe finden Sie verschiedene Varianten der Bessel-Funktion, die insbesondere für Schwingungsberechnungen benutzt werden. Hinzu kommt eine ganze Reihe von Umwandlungsfunktionen, um Werte zwischen den verschiedenen Zahlensystemen auszutauschen. Eine andere Gruppe hat mit den komplexen Zahlen zu tun.

Eine Tabelle zum Umwandeln von Maßeinheiten 

Ganz praktisch ist die Funktion UMWANDELN(), mit der zwischen verschiedenen Maßeinheiten umgerechnet werden kann. Sie können sich damit leicht eine Tabelle aufbauen, die die gewünschten Umwandlungen für die Maßeinheiten liefert, mit denen Sie öfters zu tun haben.

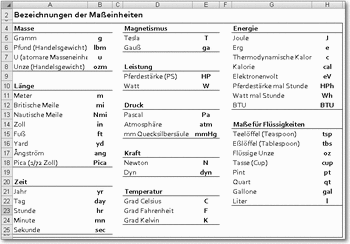
Bezeichnungen der Maßeinheiten

In der Abbildung sind die Bezeichnungen für die verfügbaren Maßeinheiten zusammengestellt. Die Bezeichnungen müssen in der Funktion jeweils mit Anführungszeichen eingegeben werden, es sei denn, Sie verwenden einen Zellbezug.

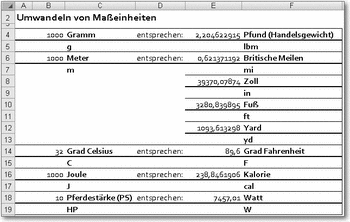
In der folgenden Tabelle benötigen Sie in den Feldern in Spalte B nur diejenigen Werte einzugeben, die Sie umwandeln wollen. Die Formeln beziehen sich dabei jeweils auf die Bezeichnungen der Maßeinheiten.

Umrechnung einiger häufig vorkommender Maßeinheiten

Referenz der technischen Funktionen 

BESSELI()

Syntax: BESSELI(x;n)

Beispiel: BESSELI(0,5;1)

Ergebnis: 0,25789

Liefert Werte der modifizierten Besselfunktion.

Bei den Besselschen Funktionen (auch unter dem Namen Zylinderfunktionen bekannt) handelt es sich um mehrere miteinander verwandte Funktionen, die in Physik und Technik besonders bei Schwingungsberechnungen benutzt werden. Die Besselschen Funktionen finden Sie in mathematischen Tabellenwerken unter

J0(x), J1(x)..   BESSELJ() 
I0(x), I1(x)..   BESSELI() 
K0(x), K1(x)..   BESSELK() 
Y0(x), Y1(x)..   BESSELY()

meist aber nur für die nullte und erste Ordnung. Die Funktionen, die Excel 2007 bereitstellt, gestatten eine Berechnung für andere Ordnungen (mit n angegeben).

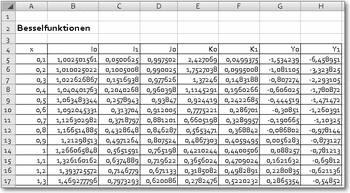
Hinweise auf die Auswirkung von n bei den verschiedenen Funktionen bietet die folgende Abbildung.

Die Bessel-Funktionen

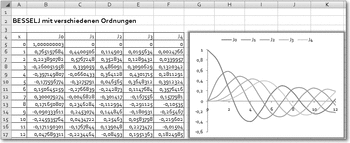
Für die Funktion BESSELJ() ist für mehrere Ordnungen der grafische Verlauf dargestellt, der sehr schön zeigt, dass die Funktion zur Berechnung gedämpfter Schwingungen geeignet ist.

Verlauf der Funktion BESSELJ()

BESSELJ()

Syntax: BESSELJ(x;n)

Beispiel: BESSELJ(0,5;2)

Ergebnis: 0,0306

Vgl. BESSELI().

BESSELK()

Syntax: BESSELK(x;n)

Beispiel: BESSELK(0,5;1)

Ergebnis: 1,65644

Vgl. BESSELI().

BESSELY()

Syntax: BESSELY(x;n)

Beispiel: BESSELY(1,3;1)

Ergebnis: -0,5485

Vgl. BESSELI().

BININDEZ()

Syntax: BININDEZ(Zahl)

Beispiel: BININDEZ(11101)

Ergebnis: 29

Liefert den Dezimalwert einer binären Zahl. Die binäre Zahl darf höchstens zehn Zeichen (0 oder 1) lang sein; bei zehn Zeichen ist das erste Zeichen das Vorzeichen-Bit (1 = negativ).

Näheres zur Zahlenumwandlung siehe DEZINBIN().

BININHEX()

Syntax: BININHEX(Zahl;Stellen)

Beispiel:BININHEX(1100)

Ergebnis: C

Liefert den Hexadezimalwert einer binären Zahl, vgl. BININDEZ().

Stellen gibt an, wie viele Stellen angezeigt werden. Ohne Angabe werden nur die notwendigen Stellen angezeigt, ist Stellen größer als diese Anzahl, dann werden führende Nullen ausgegeben.

BININOKT()

Syntax: BININOKT(Zahl;Stellen)

Beispiel: BININOKT(1100)

Ergebnis: 14

Liefert den Oktalwert einer binären Zahl, vgl. BININDEZ().

Stellen gibt an, wie viele Stellen angezeigt werden. Ohne Angabe werden nur die notwendigen Stellen angezeigt, ist Stellen größer als diese Anzahl, dann werden führende Nullen ausgegeben.

DELTA()

Syntax: DELTA(Zahl1;Zahl2)

Beispiel: DELTA(10/6;20/12)

Ergebnis: 1

Liefert 1 wenn Zahl1 und Zahl2 gleich sind, sonst 0.

DEZINBIN()

Syntax: DEZINBIN(Zahl;Stellen)

Beispiel: DEZINBIN(100)

Ergebnis: 1100100

Liefert den Binärwert einer Dezimalzahl.

Die Zahl der ausgegebenen Stellen kann mit Stellen festgelegt werden. Ohne Angabe werden nur die notwendigen Stellen, ist Stellen größer als diese Zahl, dann wird die Binärzahl mit führenden Nullen ausgegeben.

Wie die anderen Funktionen zur Zahlenumwandlung (BIN..., HEX..., OKT... und die anderen DEZ ...-Funktionen) dient DEZINBIN der Konversion von Zahlen zwischen den verschiedenen Zahlensystemen.

Zur Erinnerung: Das Dezimalsystem verfügt über 10 Ziffernzeichen (0 bis 9). Kommen Sie beim Zählen einer Zahl hinter der 9 an, dann wird der ersten Ziffer eine 0 angehängt. Sie zählen also im Binärsytem 0, 1, 10, 11, 100, im Oktalsystem 1, 2 ... 7, 10, 11, ..., 16, 20, im Hexadezimalsystem 1, 2, ... 9; A; B; C; D; E; F; 10... Im Hexadezimalsystem müssen Sie zu den bekannten Ziffern noch A bis F hinzunehmen, um insgesamt auf 16 Ziffern zu kommen.

DEZINHEX()

Syntax: DEZINHEX(Zahl;Stellen)

Beispiel: DEZINHEX(15)

Ergebnis: F

Liefert den Hexadezimalwert einer Dezimalzahl, vgl. DEZINBIN().

Die Zahl der ausgegebenen Stellen kann mit Stellen festgelegt werden. Ohne Angabe werden nur die notwendigen Stellen ausgegeben, ist Stellen größer als diese Zahl, dann wird die Hexadezimalzahl mit führenden Nullen ausgegeben.

DEZINOKT()

Syntax: DEZINOKT(Zahl;Stellen)

Beispiel: DEZINOKT(8)

Ergebnis: 10

Liefert den Oktalwert einer Dezimalzahl, vgl. DEZINBIN().

Die Zahl der ausgegebenen Stellen kann mit Stellen festgelegt werden. Ohne Angabe werden nur die notwendigen Stellen, ist Stellen größer als diese Zahl, dann wird die Binärzahl mit führenden Nullen ausgegeben.

GAUSSFEHLER()

Syntax: GAUSSFEHLER(Untere_Grenze;Obere_Grenze)

Beispiel: GAUSSFEHLER(0;1)

Ergebnis: 0,8427

Liefert Werte des Gaußschen Fehlerintegrals. Die Funktion gehört eigentlich zu den Verteilungsfunktionen der Statistik.

Mit Untere_Grenze (0 oder größer) wird der Wert angegeben, ab dem die Funktion integriert werden soll; mit Obere_Grenze der Wert, bis zu dem integriert wird. Wird Obere_Grenze nicht angegeben, wird die Integration von 0 bis Untere_Grenze durchgeführt.

GAUSSFKOMPL()

Syntax: GAUSSFKOMPL(Untere_Grenze)

Beispiel: GAUSSFKOMPL (0,8)

Ergebnis: 0,2579

Liefert komplementäre Werte des Gaußschen Fehlerintegrals, vgl. GAUSSFEHLER().

Es gilt die Beziehung:

1 – GAUSSFEHLER(x) = GAUSSFKOMPL (x)

GGANZZAHL()

Syntax: GGANZZAHL(Zahl;Schritt)

Liefert 1, wenn Zahl größer oder gleich ist als die mit Schritt angegebene Zahl, sonst 0.

HEXINBIN()

Syntax: HEXINBIN(Zahl;Stellen)

Beispiel: HEXINBIN(A)

Ergebnis: 1010

Liefert den Binärwert einer hexadezimalen Zahl, vgl. DEZINBIN().

Stellen gibt an, wie viele Stellen angezeigt werden. Ohne Angabe werden nur die notwendigen Stellen angezeigt, ist Stellen größer als diese Anzahl, dann werden führende Nullen ausgegeben.

HEXINDEZ()

Syntax: HEXINDEZ(Zahl)

Beispiel: HEXINDEZ(F)

Ergebnis: 15

Liefert den Dezimalwert einer hexadezimalen Zahl, vgl DEZINBIN().

HEXINOKT()

Syntax: HEXINOKT(Zahl;Stellen)

Beispiel: HEXINOKT(F)

Ergebnis: 17

Liefert den Oktalwert einer hexadezimalen Zahl, vgl. DEZINBIN().

Stellen gibt an, wie viele Stellen angezeigt werden. Ohne Angabe werden nur die notwendigen Stellen angezeigt, ist Stellen größer als diese Anzahl, dann werden führende Nullen ausgegeben.

IMABS()

Syntax: IMABS(Komplexe_Zahl)

Beispiel: IMABS("3+4j")

Ergebnis: 5

Liefert den Betrag einer komplexen Zahl. Die Komplexe_Zahl muss als Zeichenkette der Form:

x+aj oder x+ai

eingegeben werden, wobei x und a zwei beliebige Zahlen sein können.

Kurz einige Hinweise: Die imaginäre Einheit j (oft wird auch i geschrieben, die Funktion akzeptiert beides) ist definiert als

j = WURZEL(-1)

Auf diese Weise lassen sich aus negativen Zahlen Wurzeln ziehen: WURZEL(-25) ist 5j. Mit imaginären Zahlen lässt sich ganz normal rechnen, wenn dabei beachtet wird, dass

j^2 = –1; j^3 = -j; j^4 = 1; j^7 = -j usw.: 
4j + 2j = 6j 
4j – 4j = 0 
3j * 4j = –12 
10j/2j  = 5

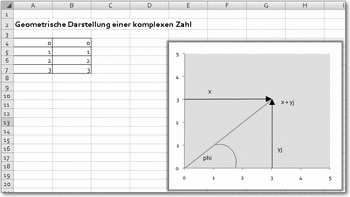
Komplexe Zahlen sind Zahlen, die aus einem reellen und einem imaginären Anteil zusammengesetzt sind. Sie lassen sich geometrisch darstellen als Punkte in einem rechtwinkligen Koordinatensystem, bei dem die waagerechte Achse die reellen (also ganz normalen) Zahlen und die senkrechte Koordinate den imaginären Anteil repräsentiert.

Geometrische Darstellung einer komplexen Zahl

Als Betrag einer komplexen Zahl gilt dann:

Betrag(x + aj) = WURZEL(x^2 + a^2) (Pythagoras)

Der Winkel phi heißt Argument der komplexen Zahl.

IMAGINÄRTEIL()

Syntax: IMAGINÄRTEIL(Komplexe_Zahl)

Beispiel: IMAGINÄRTEIL("5+12j")

Ergebnis: 12

Liefert den imaginären Anteil einer komplexen Zahl, vgl. IMABS().

IMAPOTENZ()

Syntax: IMAPOTENZ(Komplexe_Zahl;Potenz)

Beispiel: IMAPOTENZ("3+2j";2)

Ergebnis: 5+12j

Liefert die ganzzahlige Potenz einer komplexen Zahl, vgl. IMABS().

Für das Quadrat komplexer Zahlen lässt sich die Rechnung einfach nachvollziehen:

(3+2j)^2 = 9 + 12j + 4j^2 = 9 + 12j – 4

IMARGUMENT()

Syntax: IMARGUMENT(Komplexe_Zahl)

Beispiel: IMARGUMENT("3+3j")

Ergebnis: 0,785

Liefert das Argument einer komplexen Zahl, vgl. IMABS(). Der Winkel wird im Bogenmaß geliefert.

IMCOS()

Syntax: IMCOS(Komplexe_Zahl)

Beispiel: IMCOS("3+4j")

Ergebnis: -27,03 – 3,85j (gerundet)

Liefert den Cosinus einer komplexen Zahl, vgl. IMABS().

IMDIV()

Syntax: IMDIV(Komplexe_Zahl1;Komplexe_Zahl2)

Beispiel: IMDIV("12+4j";"3 – 2j")

Ergebnis: 2,15+2,77j (gerundet)

Liefert das Ergebnis der Division zweier komplexer Zahlen, vgl. IMABS().

IMEXP()

Syntax: IMEXP(Komplexe_Zahl)

Beispiel: IMEXP("0+4j")

Ergebnis: -0,65 – 0,76j (gerundet)

Liefert das Resultat der Potenzierung von e (Eulersche Zahl) mit einer komplexen Zahl, vgl. IMABS() und die mathematische Funktion EXP().

IMKONJUGIERTE()

Syntax: IMKONJUGIERTE(Komplexe_Zahl)

Beispiel: IMKONJUGIERTE("1+j")

Ergebnis: 1-j

Liefert zu einer komplexen Zahl das konjugiert komplexe Komplement. Beide Zahlen zusammen heißen »konjugiert komplex«. Geometrisch handelt es sich um eine Spiegelung an der reellen Achse, vgl. IMABS().

IMLN()

Syntax: IMLN(Komplexe_Zahl)

Beispiel: IMLN("2+2j")

Ergebnis: 1,04+0,78j (gerundet)

Liefert den natürlichen Logarithmus einer komplexen Zahl, vgl. IMABS() und die mathematische Funktion LN().

IMLOG10()

Syntax: IMLOG10(Komplexe_Zahl)

Beispiel: IMLOG10("100-j")

Ergebnis: 2,00002 – 0,00434j

Liefert den dekadischen Logarithmus einer komplexen Zahl, vgl. IMABS() und die mathematische Funktion LOG10().

IMLOG2()

Syntax: IMLOG2(Komplexe_Zahl)

Beispiel: IMLOG2("8+4j")

Ergebnis: 3,1609 – 0,6689j

Liefert den binären Logarithmus einer komplexen Zahl, vgl. IMABS() und die mathematische Funktion LOG().

IMPRODUKT()

Syntax: IMPRODUKT(Komplexe_Zahl1;Komplexe_Zahl2,...)

Beispiel: IMPRODUKT("3+4j";"3 – 4j")

Ergebnis: 25

Liefert das Produkt von bis zu 29 komplexen Zahlen, vgl. IMABS().

IMREALTEIL()

Syntax: IMREALTEIL(Komplexe_Zahl)

Beispiel: IMREALT("12-j")

Ergebnis: 12

Liefert den reellen Anteil einer komplexen Zahl, vgl. IMABS().

IMSIN()

Syntax: IMSIN(Komplexe_Zahl)

Beispiel: IMSIN("3,14+j"

Ergebnis: 0,002 – 1,175j (gerundet)

Liefert den Sinus einer komplexen Zahl, vgl. IMABS().

IMSUB()

Syntax: IMSUB(Komplexe_Zahl1;Komplexe_Zahl2)

Beispiel: IMSUB("12+2j";"3 – 2j")

Ergebnis: 9+4j

Liefert das Resultat der Subtraktion zweier komplexer Zahlen, vgl. IMABS().

IMSUMME()

Syntax: IMSUMME(Komplexe_Zahl1;Komplexe_Zahl2;...)

Beispiel: IMSUMME("1+j";"1-j")

Ergebnis: 2

Liefert die Summe von bis zu 29 komplexen Zahlen, vgl. IMABS().

IMWURZEL()

Syntax: IMWURZEL(Komplexe_Zahl)

Beispiel: IMWURZEL("3+2j")

Ergebnis: 1,82 – 0,55j (gerundet)

Liefert die Quadratwurzel einer komplexen Zahl, vgl. IMABS().

KOMPLEXE()

Syntax: KOMPLEXE(Realteil;Imaginärteil;Suffix)

Beispiel: KOMPLEXE(3;4;j)

Ergebnis: 3+4j

Bildet eine komplexe Zahl aus zwei reellen Zahlen, wobei die erste (Realteil) zum reellen, die zweite (Imaginärteil) zum imaginären Anteil wird. Mit Suffix lässt sich festlegen, ob i (»i« oder keine Angabe) oder j (»j«) zur Kennzeichnung des Imaginärteils verwendet wird, vgl. IMABS().

OKTINBIN()

Syntax: OKTINBIN(Zahl;Stellen)

Beispiel: OKTINBIN(100;10)

Ergebnis: 0001000000

Liefert den Binärwert einer oktalen Zahl, vgl. BININDEZ().

Stellen gibt an, wie viele Stellen angezeigt werden. Ohne Angabe werden nur die notwendigen Stellen angezeigt, ist Stellen größer als diese Anzahl, dann werden führende Nullen ausgegeben.

OKTINDEZ()

Syntax: OKTINDEZ(Zahl)

Beispiel: OKTINDEZ(10)

Ergebnis: 8

Liefert den Dezimalwert einer oktalen Zahl, vgl. BININDEZ().

OKTINHEX()

Syntax: OKTINHEX(Zahl;Stellen)

Beispiel: OKTINDEZ(100;6)

Ergebnis: 000040

Liefert den hexadezimalen Wert einer oktalen Zahl, vgl. BININDEZ().

Stellen gibt an, wie viele Stellen angezeigt werden. Ohne Angabe werden nur die notwendigen Stellen angezeigt, ist Stellen größer als diese Anzahl, dann werden führende Nullen ausgegeben.

UMWANDELN()

Syntax: UMWANDELN(Zahl;Von_Maßeinheit;In_Maßeinheit)

Beispiel: UMWANDELN(4;"J";"cal")

Ergebnis: 0,955

Liefert Umrechnungen zwischen verschiedenen Maßeinheiten. Mit Zahl wird angegeben, wie viele Einheiten der Von_Maßeinheit umgerechnet werden sollen. Von_Maßeinheit ist die Einheit, aus der umgerechnet wird; In_Maßeinheit ist die Einheit, in die umgerechnet werden soll. Welche Einheiten zur Umrechnung verfügbar sind, zeigt die Tabelle auf Seite 744.

Ihre Meinung

Wie hat Ihnen das Openbook gefallen? Wir freuen uns immer über Ihre Rückmeldung. Schreiben Sie uns gerne Ihr Feedback als E-Mail an kommunikation@rheinwerk-verlag.de.