15.4 Mathematische Funktionen 

Angesichts der Fülle von Funktionen aus den Bereichen von Mathematik und Trigonometrie sind einige Vorbemerkungen nötig.
Trigonometrische Funktionen 
Die Winkelfunktionen, die nicht nur in der Geometrie, sondern auch in all jenen wissenschaftlichen Bereichen benötigt werden, die sich mit Schwingungen im weitesten Sinne (Schall, Licht, Elektrizität, Mechanik) befassen, verdanken sich ursprünglich Berechnungen am rechtwinkligen Dreieck.
Trigonometrische Funktionen
Gearbeitet wird mit Winkelgrößen, die nicht in Grad, sondern in Bogenmaß angegeben sind. Als Bogenmaß eines Winkels wird die Länge des Kreisbogens bezeichnet, den der Winkel aus dem Einheitskreis (Kreis mit dem Radius 1) ausschneidet. Da der Umfang eines Kreises 2*r*PI ist, beträgt der Umfang des Einheitskreises 2*PI, das Bogenmaß des Winkels 360 Grad ist also 2*PI.
Die Umrechnung von Grad in Bogenmaß ist demnach:
Grad = Bogenmaß*180/PI Bogenmaß = Grad*PI/180
Die Winkelfunktionen geben die Verhältnisse bestimmter Seiten eines rechtwinkligen Dreiecks in Abhängigkeit von einem Winkel an:
SIN(x) = Gegenkathete/Hypothenuse COS(x) = Ankathete/Hypothenuse TAN(x) = Gegenkathete/Ankathete COT(x) = Ankathete/Gegenkathete
Der Cotangens ist als Funktion in Excel nicht enthalten, da er der Kehrwert des Tangens ist:
COT(x) = 1/TAN(x)
Mit den jeweiligen Arcus-Funktionen wird ausgehend von einer Winkelfunktion der zugehörige Winkel im Bogenmaß (= Arcus) ermittelt. Es gilt also für alle Winkelfunktionen eine Beziehung nach dem Muster:
Wenn y = SIN(x) dann gilt ARCSIN(y) = x
Hyperbolische Funktionen 
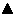
Die hyperbolischen Funktionen sind, trotz ihrer an Winkelfunktionen erinnernden Namen, keine eigentlichen Winkelfunktionen. Das wird schon daran deutlich, dass sie im Gegensatz zu Winkelfunktionen nicht periodisch verlaufen. Die Namensgebung rechtfertigt sich aber aus einer großen formalen Übereinstimmung bei den Beziehungen zwischen den einzelnen Funktionen sowie aus mathematischen Zusammenhängen zwischen beiden. Anwendung finden derartige Funktionen z. B. in einigen statistischen Näherungsverfahren, bei statischen Berechnungen und in der Analysis.
Hyperbolische Funktionen
Die Bezeichnung der inversen Funktionen (Area-Funktionen) mit ARC ... (analog zu den Arcus-Funktionen der Winkelfunktionen) ist allerdings sehr unglücklich: die Area-Funktionen liefern keinen Winkel im Bogenmaß (Arcus), sondern in der geometrischen Deutung eine Fläche. Der Cotangens hyperbolicus ist in Excel nicht eigens als Funktion enthalten, da er der Kehrwert des Tangens hyperbolicus ist:
coth(x) = 1/tanh(x)
Für die Area-Funktionen gilt (analog zu den Winkelfunktionen) für alle hyperbolischen Funktionen eine Beziehung nach dem Muster:
Wenn y = SINHYP(x) dann gilt ARCSINHYP(y) = x
Referenz der mathematische Funktionen 
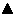
ABRUNDEN()
Syntax: ABRUNDEN(Zahl;Anzahl_Stellen)Beispiel: ABRUNDEN(-657,65;-1)Ergebnis: -650Die Funktion rundet eine Zahl in Richtung 0 auf dem Zahlenstrahl. Positive Zahlen werden also abgerundet, negative aufgerundet.
Mit dem Argument Anzahl_Stellen wird die Anzahl der Stellen angegeben, die beim Runden berücksichtigt wird. Ist Anzahl_Stellen gleich 1 oder größer, dann wird auf die entsprechende Anzahl Dezimalstellen abgeschnitten, ist es Null, dann werden die Dezimalstellen abgeschnitten, sodass die Ganzzahl übrig bleibt. Ist das Argument negativ, wird um die angegebenen Stellen nach links gerundet, und zwar so, dass sich die gerundete Zahl in Richtung Null bewegt.
ABS()
Syntax: ABS(Zahl)Beispiel: ABS(-8)Ergebnis: 8Diese Funktion eliminiert die Vorzeichen von Zahlenwerten. Ob ABS auf Zahlen mit negativem oder positivem Vorzeichen angewendet wird, als Ergebnis wird der nicht negative Betrag dieser Zahlen geliefert (in mathematischer Schreibweise |x|).
ARCCOS()
Syntax: ARCCOS(Zahl)Beispiel: ARCCOS(0,9)Ergebnis: 0,451026Die Funktion ARCCOS ergibt zu dem gegebenen Cosinus eines Winkels den zugehörigen Winkel im Bogenmaß. Für Cosinuswerte zwischen –1 und 1 liegt der Winkel zwischen 0 und PI.
Soll der Winkel in Grad angegeben werden, müsste die Formel im Beispiel lauten:
ARCCOS(0,9)*180/PI()
Das Ergebnis ist dann 25,84 Grad.
ARCCOSHYP()
Syntax: ARCCOSHYP(Zahl)Beispiel: ARCCOSHYP(1)Ergebnis: 0Umkehrfunktion zu COSHYP().
ARCSIN()
Syntax: ARCSIN(Zahl)Beispiel: ARCSIN(0,5)Ergebnis: 0,523598ARCSIN berechnet zu einem gegebenen Sinuswert den zugehörigen Winkel. Für Sinuswerte zwischen –1 und 1 liegt der Winkel zwischen -PI/2 und PI/2, d. h. zwischen –90 und 90 Grad.
ARCSINHYP()
Syntax: ARCSINHYP(Zahl)Beispiel: ARCSINHYP(2)Ergebnis: 1,443635Umkehrfunktion zu SINHYP().
ARCTAN()
Syntax: ARCTAN(Zahl)Beispiel: ARCTAN(0,3)Ergebnis: 0,291456Mit ARCTAN wird zu dem gegebenen Tangens eines Winkels der Winkel errechnet. Für Tangenswerte zwischen 0 und unendlich liegt der Winkel zwischen 0 und PI/2.
ARCTAN2()
Syntax: ARCTAN2(x_Koordinate;y_Koordinate)Beispiel: ARCTAN2(4;-3)Ergebnis: -0,643501Diese spezielle Form des Arcustangens gestattet es, bei einer Geraden, die durch den 0-Punkt eines Koordinatenkreuzes verläuft, direkt durch Angabe von x-Koordinate und y-Koordinate eines Punkts den Steigungswinkel der Geraden zu ermitteln. Das Ergebnis liegt zwischen PI und -PI.
ARCTANHYP()
Syntax: ARCTANHYP(Zahl)Beispiel: ARCTANHYP(0,5)Ergebnis: 0,54930Umkehrfunktion zu TANHYP().
AUFRUNDEN()
Syntax: AUFRUNDEN(Zahl;Anzahl_Stellen)Beispiel: AUFRUNDEN(2,356;2)Ergebnis: 2,36Die Funktion rundet eine Zahl von der Null weg. Mit dem Argument Anzahl_Stellen wird die Anzahl der Stellen angegeben, die beim Runden berücksichtigt wird. Ist Anzahl_Stellen gleich 1 oder größer, dann wird auf die entsprechende Anzahl Dezimalstellen aufgerundet, ist es Null, dann wird auf die nächste Ganzzahl aufgerundet, ist es negativ, dann wird die entsprechende Ziffer links vom Dezimalzeichen aufgerundet.
BOGENMASS()
Syntax: BOGENMASS(Winkel)Beispiel: BOGENMASS(180)Ergebnis: 3,14Die Funktion wandelt den Gradwert des angegebenen Winkels in Bogenmaß (Radiant) um.
COS()
Syntax: COS(Zahl)Beispiel: COS(PI()/6)Ergebnis: 0,866025Die Funktion berechnet den Cosinus eines Winkels (im Beispiel 30 Grad). Der Winkel wird im Bogenmaß angegeben. Das Ergebnis liegt zwischen –1 und 1.
COSHYP()
Syntax: COSHYP(Zahl)Beispiel: COSHYP(1,5)Ergebnis: 2,352410COSHYP(x) = (e^x + e^-x)/2
x liegt zwischen -unendlich und unendlich, COSHYP(x) zwischen 1 und unendlich.
EXP()
Syntax: EXP(Zahl)Beispiel: EXP(2)Ergebnis: 7,3890561Die Eulersche Zahl e (2,71828...) wird mit Zahl potenziert. Da e die Basis der natürlichen Logarithmen ist, ergibt EXP(1) den Wert von e (2,71828...). EXP(LN(x)) liefert den Wert x. EXP ist die Umkehrfunktion von LN. Die Funktion EXP wird in erster Linie zur Beschreibung von Wachstumsfunktionen verwendet.
FAKULTÄT()
Syntax: FAKULTÄT(Zahl)Beispiel: FAKULTÄT(4)Ergebnis: 24 (=1*2*3*4)Die Fakultät einer Zahl (in der Mathematik geschrieben 3! für Fakultät von 3) ist das Produkt 1*2*3*4*...*Zahl. Anwendungsbereich ist die Kombinatorik, in der im weitesten Sinne die Frage gestellt wird, wie viele Möglichkeiten es gibt, Elemente aus einer Menge zu kombinieren. Hier nur ein Beispiel: Wie viele Möglichkeiten gibt es, 6 verschiedene Zahlen von 49 im Lotto auszuwählen?
= FAKULTÄT(49)/((FAKULTÄT(6)*FAKULTÄT(49–6))
Ergebnis: 13 983 816, d. h., es gibt über 13 Mio. Möglichkeiten, 6 Zahlen auf einem Lottoschein anzukreuzen, und so viele Kombinationen müssten durchgespielt werden, um ganz sicher »6 Richtige« im Lotto zu haben.
GANZZAHL()
Syntax: GANZZAHL(Zahl)Beispiel: GANZZAHL(5,7)Ergebnis: 5Ein numerischer Ausdruck wird auf die nächstkleinere ganze Zahl reduziert, die Nachkommastellen werden gleichsam abgeschnitten. Negative Zahlen werden von 0 weg, also zur nächsten kleineren Zahl gerundet. GANZZAHL(-5,7) ergibt also –6.
GERADE()
Syntax: GERADE(Zahl)Beispiel: GERADE(-3)Ergebnis: -4Die Funktion rundet Zahlen zur nächsten geraden Ganzzahl weg von 0 und ist damit komplementär zur Funktion UNGERADE. Wenn Zahl schon eine gerade ganze Zahl ist, dann wird dieser Wert wiedergegeben.
GGT()
Syntax: GGT(Zahl1;Zahl2;...)Beispiel: GGT(56;98)Ergebnis: 14Liefert den größten gemeinsamen Teiler von zwei oder mehreren ganzen Zahlen.
Ein gemeinsamer Teiler ist eine Zahl, durch die alle angegebenen Zahlen geteilt werden können, ohne dass ein Rest bleibt. Der größte gemeinsame Teiler ist die größte derartige Zahl.
GRAD()
Syntax: GRAD(Winkel)Beispiel: GRAD(PI()/3)Ergebnis: 60Winkelangaben werden aus dem Bogenmaß (Radiant oder als Einheit rad) in Grad übertragen. Für die Konversion gilt die Formel:
Grad=rad*360/(2*PI).
KGV()
Syntax: KGV(Zahl1;Zahl2;...)Beispiel: KGV(3;4;5;10)Ergebnis: 60Liefert das kleinste gemeinsame Vielfache der angegebenen Zahlen.
Das kleinste gemeinsame Vielfache ist die kleinste Zahl, die durch alle angegebenen Zahlen ohne Rest teilbar ist.
KOMBINATIONEN()
Syntax: KOMBINATIONEN(n;k)Beispiel: KOMBINATIONEN(7;3)Ergebnis: 35Die Funktion gibt den Wert des Binomialkoeffizienten aus. KOMBINATIONEN() rechnet nach der Formel
n! / (k! * (n-k)!)
Die Funktion beantwortet die Frage, wie viele Gruppen der Größe k aus n Elementen gebildet werden können, wenn die Reihenfolge keine Rolle spielt.
Werden keine ganzen Zahlen eingegeben, so werden sie zu GANZZAHL abgeschnitten, 5,456 ergibt dann 5. Wenn die Argumente kleiner Null eingegeben werden und n kleiner als k sein sollte, wird eine Fehlermeldung ausgegeben.
Wollen Sie etwa berechnen, wie viele Möglichkeiten es gibt, 6 Zahlen von 49 anzukreuzen, dann liefert KOMBINATIONEN(49;6) das Ergebnis 13 983 816 (vgl. FAKULTÄT).
KÜRZEN()
Syntax: KÜRZEN(Zahl;Anzahl_Stellen)Beispiel: KÜRZEN(5,7)Ergebnis: 5Ein numerischer Ausdruck wird auf die mit Anzahl_Stellen angegebenen Stellen verkürzt, d. h., die Stellen hinter dem Komma werden abgeschnitten. Wird Anzahl_Stellen nicht angegeben, so wird das Argument als 0 angenommen und der ganzzahlige Rest wiedergegeben. Dies gilt auch (im Gegensatz zu GANZZAHL) bei negativen Zahlen: KÜRZEN(-5,7) ergibt –5.
LN()
Syntax: LN(Zahl)Beispiel: LN(10)Ergebnis: 2,30258509LN() ist der natürliche Logarithmus einer Zahl, d. h. derjenige Wert, mit dem die Eulersche Zahl potenziert werden müsste, damit die Zahl als Ergebnis herauskommt. Die Anwendung liegt ähnlich wie bei der Funktion EXP() im Bereich von Wachstumsprozessen in Naturwissenschaft und Technik.
LOG()
Syntax: LOG(Zahl;Basis)Beispiel: LOG(4;2)Ergebnis: 2LOG ist von allen Logarithmusfunktionen, die Excel bereitstellt, die allgemeinste. Sie gestattet es, den Logarithmus einer Zahl zu jeder beliebigen Basis zu ermitteln, wobei das Ergebnis immer derjenige Wert ist, mit dem die Basis potenziert werden müsste, um die Zahl zu erhalten.
LOG(Zahl;2) ergibt den binären Logarithmus LOG(Zahl;EXP(1)) ergibt den natürlichen Logarithmus; LOG(Zahl;10) ergibt den dekadischen Logarithmus.
Wird auf die Angabe einer Basis verzichtet, dann nimmt Excel als Basis 10 an (das entspricht der folgenden Funktion LOG10).
Zur Erinnerung hier einige der Rechenregeln, die für alle Logarithmen gelten:
LOG(a;a)=1 (der Logarithmus der Basis ist 1) LOG(1)=0 (Unabhängig von der Basis ist der Logarithmus von 1 gleich 0) LOG(a*b)=LOG(a)+LOG(b) LOG(a/b)=LOG(a)-LOG(b)
d. h., Multiplikation und Division werden auf logarithmischer Ebene auf Addition und Subtraktion zurückgeführt.
LOG(a^n)=n*LOG(a) (Potenzen werden auf logarithmischer Ebene auf Multiplikationen zurückgeführt).
LOG10()
Syntax: LOG10(Zahl)Beispiel: LOG10(4)Ergebnis: 0,60205999Der dekadische Logrithmus einer Zahl, d. h., der Wert, mit dem 10 potenziert werden müsste, um die Zahl zu erhalten. LOG10(100)=2, d. h., 10 muss zum Quadrat genommen werden, um 100 zu erhalten.
MDET()
Syntax: MDET(Matrix)Beispiel: MDET({2.3;4.5})Ergebnis: -2Die Ermittlung der Determinante einer Matrix wird benötigt bei der Lösung von linearen Gleichungen mit mehreren Unbekannten. Gleichungen dieser Art kommen unter anderem im naturwissenschaftlich-technischen Bereich (z. B. Berechnung von Widerstandsnetzwerken) und in der Ökonomie (z. B. Optimierungsaufgaben, die von mehreren Faktoren abhängen) vor.
Die Lösung derartiger Gleichungssysteme ist »von Hand« eine äußerst zeitraubende Angelegenheit, über die Bildung von Determinanten dagegen einfacher erledigt. In Excel lassen sich derartige Aufgaben allerdings wesentlich schneller mit dem Solver bearbeiten.
MINV()
Syntax: MINV(Matrix)Beispiel: MINV({2.3;4.5})Ergebnis: {-2,5.1,5;2.-1}Bildet die Inverse zu einer Matrix. Die Funktion findet Anwendung bei der Lösung von Gleichungssystemen mit mehreren Unbekannten (vgl. MDET).
MMULT()
Syntax: MMULT(Matrix1;Matrix2)Beispiel: MMULT({2.3;4.5};{6.7;8.9})Ergebnis: {36.41;64.73}Liefert das Produkt zweier Matrizen. Die Spalten von Matrix1 müssen in der Anzahl mit den Zeilen von Matrix2 übereinstimmen.
OBERGRENZE()
Syntax: OBERGRENZE(Zahl,Schritt)Beispiel: OBERGRENZE(2,2434;0,05)Ergebnis: 2,25Die Funktion rundet den Wert Zahl auf das nächste Vielfache von Schritt auf und ist damit komplementär zu UNTERGRENZE.
Mit dem Wert 0,05 für Schritt kann z. B. bestimmt werden, dass die Hundertstelstelle beim Aufrunden immer nur eine 5 oder eine Null sein kann. Mit einem Wert 0,5 für Schritt wird dafür gesorgt, dass z. B. nicht mehr in Cent, sondern nur noch für 5-Cent-Stücke ausgepreist wird.
Aufrunden meint im Sinne dieser Funktion, dass immer von Null weg gerundet wird, z. B. wird OBERGRENZE(-4,2546;-0,5) zu –4,5. Bei unterschiedlichen Vorzeichen für Zahl und Schritt wird eine Fehlermeldung ausgegeben.
PI()
Syntax: PI()Beispiel: PI()Ergebnis: 3,14159265358979Die Funktion PI liefert den numerischen Wert von PI. Neben der Umrechnung von Winkeln von Grad in Bogenmaß wird PI unter anderem für Kreis- und Kugelberechnungen benötigt. Obwohl für PI als Verhältniszahl kein Argument angegeben wird, benötigt Excel die beiden Klammern hinter dem Funktionsnamen.
Kreisumfang: U=2*r*PI() Kreisfläche: A=r^2*PI() Kugeloberfläche: O=4*r^2*PI() Kugelvolumen: V=4/3*r^3*PI()
POLYNOMIAL()
Syntax: POLYNOMIAL(Zahl1;Zahl2;...)Beispiel: POLYNOMIAL(3;4;5)Ergebnis: 27720Liefert die Fakultät der Summe der Argumente geteilt durch das Produkt der Fakultäten, also
(Zahl1+Zahl2...)! / Zahl1!*Zahl2!...
Die Funktion kann in der Kombinatorik nützlich sein.
POTENZ()
Syntax: POTENZ(Zahl;Potenz)Beispiel: POTENZ(2;10)Ergebnis: 1024Die Funktion gibt als Ergebnis die Potenzierung einer Zahl aus. Dabei wird dasselbe Rechenverfahren verwendet, das auch mit dem Operatorzeichen »^« zur Anwendung kommt. Statt 4^2 kann also auch POTENZ(4;2) eingegeben werden.
POTENZREIHE()
Syntax: POTENZREIHE(x;n;m;Koeffizienten)Beispiel: POTENZREIHE(3;1;1;{2;3;4})Ergebnis: 141Liefert eine Summe von Potenzen der Zahl x. Berechnet wird nach der Formel:
a1*x^n + a2*x^(n+m) + a3*x^(n+2m) ...
wobei a1, a2, ... mit Koeffizienten angegeben wird. Die Zahl der hier eingetragenen Werte liefert zugleich die Zahl der Summanden in der Formel.
Mit dieser Funktion lassen sich gut Näherungsberechnungen für Funktionen durchführen.
PRODUKT()
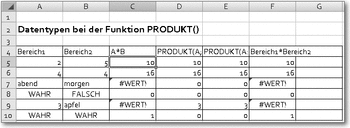
Syntax: PRODUKT(Zahl1;Zahl2;...)Beispiel: PRODUKT(4;5;6)Ergebnis: 120Die Argumente (Zahl1, Zahl2 bis Zahl30) werden miteinander multipliziert. Wie unterschiedliche Datentypen bei der Funktion PRODUKT behandelt werden, zeigt die folgende Abbildung.
Datentypen bei der Funktion Produkt
QUADRATESUMME()
Syntax: QUADRATESUMME(Zahl1;Zahl2;...)Beispiel: QUADRATESUMME(2;3;4)Ergebnis: 29Die Funktion berechnet die Summe der Quadrate der einzelnen Werte. Außer Zahlen können auch numerische Formeln oder die Adressen von Bereichen dort stehen, die auf Zahlen oder numerische Formeln verweisen.
QUOTIENT()
Syntax: QUOTIENT(Zähler;Nenner)Beispiel: QUOTIENT(15;6)Ergebnis: 2Liefert das ganzzahlige Ergebnis einer Division; der Rest wird weggelassen.
RADIANT()
Syntax: RADIANT(Winkel)Beispiel: RADIANT(57,296)Ergebnis: 1Das Ergebnis ist der Radiant, Einheitszeichen rad oder auch das Bogenmaß eines Winkels. Im Bogenmaß wird das Verhältnis von Kreisbogen und Radius angegeben. Für die Berechnung gilt:
rad = 2*PI*Winkel/360.
REST()
Syntax: REST(Zahl;Divisor)Beispiel: REST(25;6)Ergebnis: 1Der Restbetrag (Modulus) bei der Division Zahl/Divisor. Der Divisor muss ein anderer Wert als Null sein, das Vorzeichen des Ergebnisses ist immer das des Divisors. Ist Zahl 0, so ist das Ergebnis auch 0.
RÖMISCH()
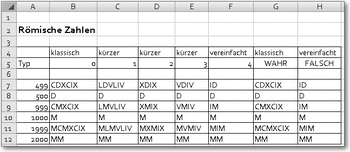
Syntax: RÖMISCH(Zahl;Typ)Beispiel: RÖMISCH(88)Ergebnis: LXXXVIIIWandelt Zahlen in Zeichenketten um, die der römischen Zahlendarstellung entsprechen. Mit Typ kann festgelegt werden, nach welchem Schema umgewandelt wird: 0 oder nicht festgelegt ergibt den klassischen Typus, 1,2 und 3 ergibt eine verkürzte Form, 4 die vereinfachte. Ist für Typ WAHR gesetzt, erhalten Sie den klassischen Typ, FALSCH ergibt den vereinfachten.
Beispiele für die Umwandlung in römische Zahlen
RUNDEN()
Syntax: RUNDEN(Zahl;Anzahl_Stellen)Beispiel: RUNDEN(3,45678;2)Ergebnis: 3,46Eine Zahl wird auf die durch Stellen angegebene Stellenzahl auf- oder abgerundet. Ist die zu rundende Dezimalstelle 5, dann wird von 0 weg gerundet. (RUNDEN(3,45;1) ergibt 3,5). Ist Zahl = 0, wird auf eine Ganzzahl gerundet, im Unterschied zur Funktion GANZZAHL, die die Nachkommastellen abschneidet.
SIN()
Syntax: SIN(Zahl)Beispiel: SIN(PI()/6)Ergebnis: 0,5Die Funktion berechnet den Sinus eines Winkels (im Beispiel 30 Grad). Der Winkel wird im Bogenmaß angegeben. Das Ergebnis liegt zwischen –1 und 1.
SINHYP()
Syntax: SINHYP(Zahl)Beispiel: SINHYP(1,5)Ergebnis: 2,129279SINHYP(x) = (e^x – e^-x)/2
x liegt zwischen -unendlich und unendlich, SINHYP(x) zwischen -unendlich und unendlich.
SUMME()
Syntax: SUMME(Zahl1;Zahl2;...)Beispiel: SUMME(4;4,5;5)Ergebnis: 13,5Die Summe der Argumente wird berechnet. Insgesamt sind 30 Argumente erlaubt. Wie sich unterschiedliche Datentypen auswirken, zeigt die folgende Tabelle. Auch hier ergeben sich wieder Unterschiede (analog zu PRODUKT()) zu den Ergebnissen von Formeln, die mit »+« aufgebaut sind.
Datentypen bei der Funktion SUMME()
SUMMENPRODUKT()
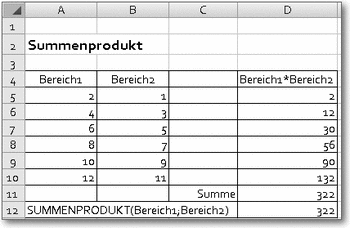
Syntax: SUMMENPRODUKT(Matrix1;Matrix2;Matrix3;...)Beispiel: SUMMENPRODUKT({4.5.6};{1.2.3})Ergebnis: 32 für(4*1+5*2+6*3)Die einzelnen Elemente der als Argumente angegebenen Matrizen werden der Reihe nach miteinander multipliziert, anschließend werden die Multiplikationsergebnisse summiert. Sie müssen von der Zeilenanzahl und der Spaltenanzahl her gleich sein. Es handelt sich also nicht um ein Summenprodukt, sondern um eine Produktensumme.
Diese Funktion ist immer dann nützlich, wenn die einzelnen Produkte nicht angezeigt werden müssen oder sollen, sondern nur die Endsumme. Als Argumente werden natürlich normalerweise (wie in den meisten Funktionen) Bereichsnamen oder Bereichsadressen angegeben, wie das folgende Beispiel demonstriert:
Die Funktion Summenprodukt
SUMMEWENN()
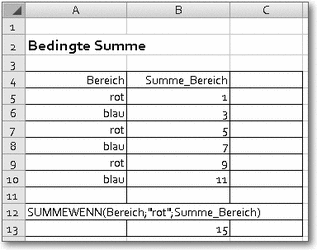
Syntax: SUMMEWENN(Bereich;Suchkriterien;Summe_Bereich)Beispiel: siehe AbbildungDie Funktion vergleicht die Werte von Bereich mit dem Wert von Suchkriterien. Werden Werte in Bereich gefunden, die dem Kriterium entsprechen, sucht die Funktion nach korrespondierenden Werten in einem zweiten Bereich (Summe_Bereich) und summiert diese auf. Wird kein Wert gefunden, der dem Kriterium entspricht, wird 0 ausgegeben. Wird Summe_Bereich nicht angegeben, wird Bereich aufsummiert.
Bedingte Summenbildung
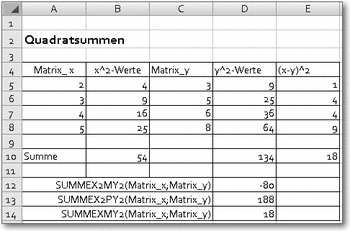
SUMMEX2MY2()
Syntax: SUMMEX2MY2(Matrix_x;Matrix_y)Beispiel: siehe AbbildungDie Funktion subtrahiert die Summen der quadrierten x-Werte und der quadrierten y-Werte. (Der Name der Funktion meint Summe x^2 Minus y^2).
Um die Arbeitsweise der Funktion zu erläutern, wurde in der Beispieltabelle eine Spalte für x^2-Werte und eine für y^2-Werte angelegt. Die Summen der Spalten voneinander abgezogen geben das Resultat der Funktion wieder. Für die Funktion selbst werden als Argumente nur die x- und die y-Werte benötigt.
Die Spalten für die Argumente müssen dieselbe Größe haben, sonst wird eine Fehlermeldung ausgegeben. Diese und die anderen beiden (zusammengehörenden) Funktionen werden besonders häufig für statistische Anwendungen benötigt.
Quadratsummen
SUMMEX2PY2()
Syntax: SUMMEX2PY2(Matrix_x;Matrix_y)Beispiel: siehe SUMMEX2MY2Ergebnis: 188Diese Funktion addiert die Summen der quadrierten x-Werte und der quadrierten y-Werte.
Die Spalten für die Argumente müssen dieselbe Größe haben, sonst wird eine Fehlermeldung ausgegeben. Diese und die anderen beiden (zusammengehörenden) Funktionen werden besonders häufig für statistische Anwendungen benötigt.
SUMMEXMY2()
Syntax: SUMMEXMY2(Matrix_x;Matrix_y)Beispiel: siehe SUMMEX2MY2()Ergebnis: 18Die Differenz zwischen x-Werten und y-Werten wird ausquadriert und die einzelnen Werte werden dann aufsummiert.
Die Spalten für die Argumente müssen dieselbe Größe haben, sonst wird eine Fehlermeldung ausgegeben. Diese und die anderen beiden vorhergehenden Funktionen werden besonders häufig für statistische Anwendungen benötigt.
TAN()
Syntax: TAN(Zahl)Beispiel: TAN(PI()/6)Ergebnis: 0,577350Die Funktion berechnet den Tangens eines Winkels (im Beispiel 30 Grad). Der Winkel wird im Bogenmaß angegeben. Das Ergebnis liegt zwischen 0 und unendlich.
TANHYP()
Syntax: TANHYP(Zahl)Beispiel: TANHYP(1,5)Ergebnis: 0,905148TANHYP(x) = (e^x – e^-x)/(e^x + e^-x)
x liegt zwischen -unendlich und unendlich, TANHYP(x) zwischen –1 und 1.
Der hyperbolische Cotangens errechnet sich analog zu den Winkelfunktionen als 1/TANHYP().
TEILERGEBNIS()
Syntax: TEILERGEBNIS(Funktion;Bezug1;Bezug2;...)Beispiel: TEILERGEBNIS(4;A10:A13)Ergebnis: 7, wenn in A10:A13 die Werte 4,7,6,5 stehenDie Funktion gibt ein Teilergebnis aus einer Liste oder Datenbank zurück. Gleiche Ergebnisse erzielen Sie auch mit dem Menübefehl Daten/Teilergebnisse. Funktion gibt mittels einer Nummer von 1 bis 11 eine Funktion an, mit der die Teilergebnisse berechnet werden sollen:
|
1 |
MITTELWERT |
|
2 |
ANZAHL |
|
3 |
ANZAHL2 |
|
4 |
MAX |
|
5 |
MIN |
|
6 |
PRODUKT |
|
7 |
STABW |
|
8 |
STABWN |
|
9 |
SUMME |
|
10 |
VARIANZ |
|
11 |
VARIANZEN |
Bezug1 gibt den Bereich an, für den das Teilergebnis berechnet werden soll. Ausgeblendete Zeilen werden dabei ignoriert, Teilergebnisse von Teilergebnissen ebenfalls, weil sie sonst mehrfach in die Berechnung eingehen würden.
UNGERADE()
Syntax: UNGERADE(Zahl)Beispiel: UNGERADE(-5,3)Ergebnis: -7Die Funktion rundet Zahlen zur nächsten ungeraden Ganzzahl weg von 0 und ist damit komplementär zur Funktion GERADE. Wenn Zahl schon eine ungerade ganze Zahl ist, dann wird dieser Wert wiedergegeben. Das eingegebene Argument wird vom Komma weg gerundet. Für positive Zahlen ein Beispiel.
UNGERADE(5,3) ergibt 7.
UNTERGRENZE()
Syntax: UNTERGRENZE(Zahl;Schritt)Beispiel: UNTERGRENZE(3,085;0,1)Ergebnis: 3Die Funktion rundet den Wert Zahl ab auf das nächste Vielfache von Schritt und ist damit komplementär zu OBERGRENZE. Dadurch ist es möglich, Kalkulationsergebnisse so abzurunden, dass nicht nur der Wert der letzten Stelle, die angegeben wurde, gerundet wird. Mit dem Wert 0,05 für Schritt kann z. B. bestimmt werden, dass die Hundertstel-Stelle beim Abrunden immer nur eine 5 oder eine 0 sein kann. Mit einem Wert 0,5 für Schritt wird z. B. dafür gesorgt, dass nicht mehr in Cent, sondern nur noch für 5-Cent-Stücke ausgepreist wird.
Aufrunden meint im Sinne dieser Funktion, dass immer zur Null hin gerundet wird, z. B. wird UNTERGRENZE(-2,54542;0,05) gerundet zu –2,5. Bei unterschiedlichen Vorzeichen für Zahl und Schritt wird eine Fehlermeldung ausgegeben.
VORZEICHEN()
Syntax: VORZEICHEN(Zahl)Beispiel: VORZEICHEN(-6)Ergebnis: -1Die Funktion VORZEICHEN() ergibt bei positiven Zahlen 1, bei negativen Zahlen –1 und bei Null 0. Sie lässt sich immer dann anwenden, wenn Operationen vom Vorzeichen abhängig sein sollen.
Wenn etwa in der Zelle B22 die Gewinne errechnet werden, dann liefert (eingetragen z. B. in C22) die Formel WENN(VORZEICHEN(B22) = –1;Achtung, Verluste!;OK) ein OK, solange der Gewinn 0 oder größer ist. Bei negativen Gewinnen erscheint dagegen der Hinweis: Achtung, Verluste!
VRUNDEN()
Syntax: VRUNDEN(Zahl;Vielfaches)Beispiel: VRUNDEN(12;5)Ergebnis: 10Rundet eine Zahl auf das nächste erreichbare ganzzahlige Vielfache einer mit Vielfaches gegebenen Zahl. Liegt die Zahl genau zwischen zwei Vielfachen, wird aufgerundet.
WURZEL()
Syntax: WURZEL(Zahl)Beispiel: WURZEL(36)Ergebnis: 6Die Quadratwurzel einer Zahl wird ermittelt. Die Funktion ergibt immer den positiven Wert, der negative Wert (auch –6*-6 ist 36) muss im Bedarfsfall ergänzt werden. Für »höhere« Wurzeln muss die Tatsache genutzt werden, dass statt der n-ten Wurzel auch geschrieben werden kann: hoch 1/n. Die dritte Wurzel (Kubikwurzel) aus einer Zahl wird demnach geschrieben: Zahl^(1/3).
Zahl darf bei der Funktion WURZEL() keine negative Zahl sein. Soll verhindert werden, dass Zahl einen negativen Wert annimmt, kann mit der ABS-Funktion gearbeitet werden.
WURZELPI()
Syntax: WURZELPI(Zahl)Beispiel: WURZELPI(2)Ergebnis: 2,5066....Liefert die Quadratwurzel aus (Zahl * PI).
ZUFALLSBEREICH()
Syntax: ZUFALLSBEREICH(Min_Wert;Max_Wert)Beispiel: ZUFALLSBEREICH(100,200)Ergebnis: 133Mit dieser Funktion erzeugen Sie eine ganzzahlige Zufallszahl zwischen Min_Wert und Max_Wert (beide eingeschlossen).
ZUFALLSZAHL()
Syntax: ZUFALLSZAHL()Beispiel: ZUFALLSZAHL()Ergebnis: 0,75419672Diese Funktion produziert Zufallszahlen zwischen 0 und 1. Wenn Sie mit Zufallszahlen arbeiten wollen, die sich im Nachhinein nicht mehr verändern, also nicht bei jeder Neuberechnung der Tabelle ebenfalls neu berechnet werden, dann drücken Sie die Taste
![]() , wenn Sie die Funktion in der Bearbeitungszeile eingegeben haben (bevor Sie die
, wenn Sie die Funktion in der Bearbeitungszeile eingegeben haben (bevor Sie die
![]() -Taste drücken).
-Taste drücken).
Zufallszahlen anderer Größenordnungen können Sie durch entsprechende Rechenoperationen mit der generierten Zufallszahl oder mit der Funktion ZUFALLSBEREICH() erreichen:
ZUFALLSZAHL*100 eine Zufallszahl zwischen 0 und 100 ZUFALLSZAHL*100+50 eine Zufallszahl zwischen 50 und 150
ZWEIFAKULTÄT()
Syntax: ZWEIFAKULTÄT(Zahl)Beispiel: ZWEIFAKULTÄT(5)Ergebnis: 15Liefert die »Altheffnersche Fakultät« einer Zahl. Sie wird berechnet als
1 * 3 * 5 * ... * Zahl (bei ungerader Zahl) 2 * 4 * 6 * ... * Zahl (bei gerader Zahl)
Ihre Meinung
Wie hat Ihnen das Openbook gefallen? Wir freuen uns immer über Ihre Rückmeldung. Schreiben Sie uns gerne Ihr Feedback als E-Mail an kommunikation@rheinwerk-verlag.de.





 Jetzt bestellen
Jetzt bestellen



