7 Optimierungen

Mit der Zielwertsuche und dem Solver stellt Excel zwei Werkzeuge zur Verfügung, die beide bestimmte Werte suchen. Bei der Zielwertsuche können Sie angeben, zu welchem Resultat eine in eine Zelle eingetragene Formel führen soll, und Excel zurückrechnen lassen, welchen Wert eine bestimmte Vorgängerzelle annehmen muss, damit dieser Zielwert erreicht wird.

Beim Solver sind die Möglichkeiten wesentlich umfangreicher: Sie haben zwar auch hier eine Zelle für einen Zielwert, Sie können aber nicht nur einen festen Zielwert angeben, sondern auch festlegen, dass der Zielwert ein Maximum oder ein Minimum erreichen soll. Sie können damit Modelle aufbauen, mit denen beispielsweise berechnet wird, unter welchen Bedingungen der optimale Gewinn erreicht wird, oder Modelle, bei denen die geringste Abfallmenge das Ziel ist.

Bei solchen Modellen können typischerweise eine Reihe von Nebenbedingungen formuliert werden, die bei der Verfolgung des Ziels eingehalten werden müssen, etwa dass bestimmte Werte sich innerhalb eines bestimmten Bereichs bewegen müssen.

7.1 Zielwertsuche 

Bei dem, was Excel als Zielwertsuche anbietet, handelt es sich mathematisch gesehen um die Lösung einer Gleichung mit einer Unbekannten. Nun sind im Prinzip ja alle Rechenaufgaben Gleichungen mit einer Unbekannten, auch wenn dies nicht weiter auffällt: Das Ergebnis ist unbekannt.

Nehmen Sie etwa die Aufgabe, den Zins, den ein bestimmter Betrag nach einer bestimmten Zeit ergibt, auszurechnen, wobei der Betrag, der Zinssatz und die Laufzeit gegeben sind. Dies Problem wird mit der Formel gelöst:

Zins = Betrag * Zinssatz * Jahre

Zins ist hierbei die Unbekannte dieser Gleichung, die anderen Ausdrücke sind bekannt. Ohne PC würden Sie ein derartiges Problem mit dem Taschenrechner bearbeiten oder auf dem Papier rechnen. Mit der gleichen Formel kann gearbeitet werden, wenn sich die Fragestellung verändert. Ist z. B. bekannt, wie hoch der Zins sein soll und welcher Betrag für wie viele Jahre zur Verfügung steht, und ist gefragt, wie hoch dann der Zinssatz sein soll, dann muss die Gleichung nach dem Zinssatz umgestellt werden:

Zinssatz = Zins / (Betrag * Jahre)

Bei so einfachen Gleichungen ist das auch keine Schwierigkeit, bei etwas komplizierteren Angelegenheiten kann das aber schon zu einer aufwändigen und auch fehleranfälligen Aufgabe werden.

Auf diese Weise könnten Sie auch innerhalb von Excel vorgehen. Dabei würden zwei Probleme auftauchen. Zum einen müssten Sie auf die eingebauten Tabellenfunktionen von Excel verzichten, da diese Funktionen ja nicht einfach umgestellt werden können. Zum anderen müssten Sie die Gleichung von Hand umstellen (dazu muss aber das mathematische Verfahren bekannt sein), da Excel keine Methode bietet, um Gleichungen umzustellen. Diese ganze Mühe lässt sich mit der Zielwertsuche vermeiden.

Bestimmung einer maximalen Kredithöhe

Bei der Zielwertsuche rechnet Excel mit den eingebauten Funktionen, stellt aber nicht mehr die Aufgabe, aus den vorgegebenen Werten das Ergebnis zu berechnen, sondern gibt das Ergebnis vor und lässt Excel ausprobieren, wie groß für das gewünschte Ergebnis einer der anderen Werte werden muss.

Dazu ein typisches Beispiel aus der Finanzmathematik. Angenommen, Sie wollen einen größeren Kredit aufnehmen und ihn im Lauf von 20 Jahren abbezahlen. Für die jährliche Abzahlung stehen 10.000 € zur Verfügung, die Bankzinsen für einen Kredit liegen bei 8,7  %. Diese Aufgabe wird mit der Tabellenfunktion für den Barwert BW() gelöst:

= BW(8,7%;20;10000)

Die Funktion liefert einen Wert von –93  270,98 €, Sie können sich also einen Kredit in dieser Höhe leisten. Nun stellen Sie aber fest, dass Sie mit diesem Kredit nicht auskommen. Sie benötigen beispielsweise 100  000 Euro. Da die Bank über den Zinssatz mit sich nicht verhandeln lässt, gibt es nur zwei Möglichkeiten: Entweder muss die Laufzeit vergrößert werden oder der jährlich bezahlte Betrag.

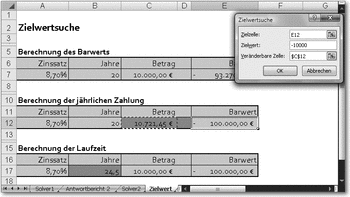
Um Ihnen die Möglichkeiten der Zielwertsuche zu zeigen, finden Sie in der nächsten Abbildung eine Tabelle, in der die Berechnung zunächst einfach zweimal kopiert worden ist, um die beiden anderen Fragen zu beantworten.

Die Überschriften für die Berechnung sind entsprechend angepasst. Um die jährlich erforderliche Zahlung für den 100  000 €-Kredit zu ermitteln, wird der Zellzeiger auf die Ergebniszelle (im Beispiel E12) gesetzt. Dann kann mit Daten/ Datentools/Was-wäre-wenn-Analyse/Zielwertsuche der Rechenprozess gestartet werden.

Zielwertsuche für ein Kreditproblem

Die Zielzelle ist schon richtig angegeben, als Zielwert wird »-100000« eingetragen. Vergessen Sie nicht das Minuszeichen, da es sich ja um eine Ausgabe handelt. Die veränderbare Zelle ist die mit der jährlichen Zahlung (im Beispiel C12). Ein Klick auf OK führt zu einem Dialogfeld, in dem Excel meldet, dass es das Problem gelöst hat. Ein weiteres OK trägt den Zielwert und den gesuchten Jahresbetrag in die Tabelle ein.

Auf die gleiche Weise lässt sich ermitteln, wie der Kredit durch eine Verlängerung der Laufzeit zu finanzieren wäre. Als Zielwert wird wieder »-100000« eingetragen, die veränderbare Zelle ist diesmal die Zelle mit der Zahl der Jahre (im Beispiel B17).

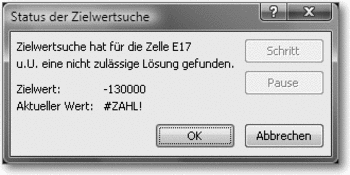
Der Versuch, auf die gleiche Weise zu ermitteln, ob durch längere Abzahlung auch ein Kredit von 130.000 € zu finanzieren wäre, führt zu einer Meldung, dass eine möglicherweise unbrauchbare Lösung gefunden wurde:

Meldung einer unbrauchbaren Lösung

Das liegt einfach daran, dass der Kredit so nicht finanzierbar wäre, da ja bei 130.000 € die jährlichen Zinsen schon über 10.000 € liegen, also für eine Tilgung gar nichts übrig bleiben würde.

Ihre Meinung

Wie hat Ihnen das Openbook gefallen? Wir freuen uns immer über Ihre Rückmeldung. Schreiben Sie uns gerne Ihr Feedback als E-Mail an kommunikation@rheinwerk-verlag.de.