15.2 Finanzmathematische Funktionen 

Neben einer Anzahl von Funktionen, die sich mit allgemeinen finanzmathematischen Themen beschäftigen, fallen vor allem drei große Gruppen von Funktionen ins Gewicht: Rentenberechnungen, Abschreibung und Wertpapiere.
Funktionen für die Rentenberechnung 
Bei Renten geht es natürlich nicht um die sozialrechtlichen Versorgungsrenten, sondern um privatwirtschaftlich vereinbarte regelmäßige Zahlungen. Die einfachste und für das Verständnis dieser Funktionen durchschaubarste Form hierfür ist folgendes Modell:
Sie zahlen auf der Bank eine bestimmte Summe an Geld ein, die dort nach einem vereinbarten Zinssatz verzinst wird. Die Bank zahlt Ihnen aus diesem Guthaben regelmäßig einen bestimmten Betrag (Rente), so lange, bis das Guthaben verbraucht ist.
Eine Anzahl von Argumenten taucht bei diesen Funktionen immer wieder auf, sodass es vernünftig scheint, diese zunächst im Zusammenhang zu besprechen.
| Funktionsargument | Erklärung |
|
Bw [Barwert] |
Der gegenwärtige rechnerische Wert einer Reihe regelmäßiger, gleich bleibender Zahlungen, z. B. einer Rente. |
|
Rmz [Ratenzahlung] |
Regelmäßig zu leistende oder zu erhaltende Zahlungen. |
|
Zins [Zinssatz] |
Das ist der Zinssatz für einen Zahlungszeitraum. Er wird dezimal (z. B. 0,08) oder als % (z. B. 8 %) angegeben. |
|
Zr [Zeitraum] |
Die einzelne Zahlungsperiode im Gesamtzeitraum.> |
|
Zw [Zukunftswert] |
Der zukünftige Wert einer Investition. Wird Zw als optionales Argument verwandt, dann wird es von Excel bei Nichteintrag mit 0 gesetzt. |
|
Zzr [Zahlungszeiträume] |
Anzahl der Zahlungsperioden. Es ist darauf zu achten, dass die Zzr mit den anderen Argumenten in den Einheiten übereinstimmen, d.h., dass einheitlich Jahre, Monate oder Tage in einer Funktion verwendet werden. Werden z. B. Monate verwendet, dann muss auch der Monatszins (Jahreszins/12) eingesetzt werden.
Beachten Sie hierbei bitte, dass in Deutschland das Zinsjahr in 12 Zinsmonate mit jeweils 30 Tagen eingeteilt wird. In anderen Ländern gelten teilweise andere Regelungen. |
|
F [Fälligkeit] |
Das Argument F für Fälligkeit legt fest, ob die Berechnung für vorschüssige oder nachschüssige Rentenzahlungen etc. erfolgen soll. Wird F nicht angegeben oder mit 0, dann wird die Funktion als nachschüssig berechnet, die Zahlungen erfolgen also am Ende der Periode. Wird F mit 1 angegeben, so erfolgt die Berechnung für eine vorschüssige Rente. |
Die Berechnung von Abschreibungen 
Bei der Abschreibung handelt es sich darum, dass eine Investition, z. B. in Maschinen, Fahrzeugen, Gebäuden etc., in zweierlei Hinsicht betriebswirtschaftlich zu berücksichtigen ist. Zum einen ist es betriebsintern so, dass mit einer Anschaffung das Anlagevermögen zunächst um den Wert dieser Anschaffung vermehrt wird, dass aber der Wert dieser Anschaffung durch Abnutzung kontinuierlich sinkt, bis am Ende der Schrottwert übrig bleibt.
Zum anderen kann eine derartige Investition von der Steuer abgesetzt werden. Die einfachste Form ist hierbei, dass die Anschaffung in dem Jahr, in dem sie getätigt wird, in vollem Umfang steuerlich geltend gemacht wird – hierzu bedarf es natürlich keiner weiteren Berechnungen. Bei langlebigen Investitionen ist es dagegen üblich, die Abschreibung auf mehrere Jahre zu verteilen.
Hierfür gibt es verschiedene Verfahren. Das einfachste ist die lineare Abschreibung: Der abzuschreibende Betrag wird gleichmäßig auf den gesamten Abschreibungszeitraum verteilt. Die anderen Verfahren, für die Excel Funktionen zur Verfügung stellt, sind so genannte degressive Abschreibungen: Der Abschreibungsbetrag sinkt von Jahr zu Jahr, sodass am Anfang ein großer Betrag abgeschrieben wird, in den folgenden Jahren wird der Betrag kontinuierlich kleiner. Auf die Frage, welche Methode am sinnvollsten und welche steuerrechtlich zulässig ist, kann Excel 2007 natürlich keine Antwort geben.
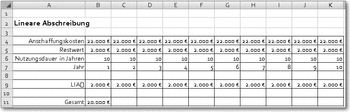
Beispiel für die Berechnung der Abschreibung 
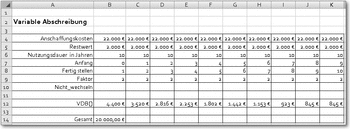
In diesem Abschnitt wird ein Tabellenblatt aufgebaut, mit dessen Hilfe Sie die Abschreibungsrate für jedes Jahr der Nutzungsdauer für ein beliebiges Wirtschaftsgut berechnen können. Um Ihnen die Entscheidung zu erleichtern, welche Abschreibungsmethode gewählt werden sollte, werden die verschiedenen Abläufe in Spalten nebeneinander gestellt. Außerdem soll das Tabellenblatt über eine Formel prüfen, ob der für die degressive Abschreibung gewählte Faktor, hier in Zelle C7, zu einem Ergebnis führt, das steuerlich zulässig ist.
In den Zellen C4 bis C7 werden zunächst die Daten abgelegt, die für die verschiedenen Funktionen als Argumente benötigt werden.
In der Spalte B wird dann die lineare Abschreibung für jedes Jahr der Nutzungsdauer berechnet. Die Formel ist für alle Jahre gleich und arbeitet mit den absoluten Adressen der Zellen C4 bis C6.
=LIA($CS4;$C$5;$C$6)
Bei der geometrisch-degressiven Abschreibung ist die Formel etwas komplexer, damit sie nach unten kopiert werden kann.
=GDA($C$4;$C$5;$C$6;$C$6-($A$19-A10);$C$7)
Beachten Sie, dass der Bezug, der sich auf die Jahreszahl in der jeweiligen Zeile bezieht, relativ ist, während die anderen Bezüge alle absolut sind. Ähnlich wird auch bei der Formel für die digitale Abschreibung verfahren.
=DIA($C$4;$C$5;$C$6;$C$6-($A$19-A10))
Die Formel für die vierte Methode ist etwas komplizierter.
=VDB($C$4;$C$5;$C$6;$A10-$A$10;$A11-$A$10;$C$7;FALSCH)
Wenn Sie die Spalten C und E vergleichen, sehen Sie, dass die geometrisch-degressive Methode für die beiden letzten Jahre geringere Beträge ergibt als die lineare. In diesen Jahren ist also ein Wechsel zur linearen Methode bei den vorliegenden Zahlen sinnvoll.
In Zelle E6 ist noch eine Formel entwickelt, die prüft, ob die geometrisch-degressive Abschreibung nach den Rechtsvorschriften überhaupt erlaubt ist.
Die Formel heißt:
=WENN(UND((1/C6*3)>C10/(C4-C5);30>=C10/(C4-C5));"Ja";"Nein")
Mit diesem Modell können Sie die günstigste Abschreibungsmethode herausfinden.
Um das Modell an kürzere oder längere Nutzungsdauern anzupassen, brauchen Sie vor der Zeile mit den Summen nur entsprechend viele Zeilen einzufügen oder zu löschen und die Formeln, wenn nötig, einige Zeilen weiter nach unten zu kopieren. Statt Jahr 1, 2, 3 ... können Sie auch die Jahreszahlen verwenden. Die Formeln in Spalte E brauchen den Wert, der jetzt in Zelle A20 steht, also ein Jahr, das über das letzte Jahr hinausreicht.
Funktionen für Wertpapierberechnungen 
Eine große Gruppe von Funktionen kreist um fest verzinsliche und unverzinsliche Wertpapiere. Auch hierzu einige Bemerkungen.
Fest verzinsliche Wertpapiere sind Wertpapiere, die für einen bestimmten Zeitraum Gültigkeit haben und in dieser Zeit regelmäßig verzinst werden. Das können Sparbriefe, Schuldverschreibungen, private oder öffentliche Anleihen und Obligationen sein.
Unverzinsliche Wertpapiere sind solche, die zu einem bestimmten Kurs ausgegeben und später zu einem höheren Kurs wieder zurückgenommen werden. De facto könnte natürlich auch hier von einer Verzinsung gesprochen werden, da der Wert des Papiers ja um einen bestimmten Betrag steigt, der sich durchaus auf einen jährlichen prozentualen Steigerungsbetrag umrechnen ließe.
- Ausgehend von dem Modell, dass ein derartiges Wertpapier (fest verzinslich oder unverzinslich) bei einem Geldinstitut erworben und später wieder veräußert wird, sind folgende Termine von zentraler Bedeutung:
- Der Ausgabetermin des Wertpapiers. Das ist der Termin, zu dem das Papier auf den Markt gebracht wird und ab dem sein Wertzuwachs bzw. seine Verzinsung läuft. Dieser Termin wird in den Funktionen unter dem Namen »Emission« geführt.
- Der Termin, zu dem ein Käufer ein Wertpapier erwirbt. Dieser kann mit dem Emissionstermin zusammenfallen, es kann aber auch – und das ist für die Berechnungen natürlich der interessantere Fall – ein späterer Termin sein. In den Funktionen heißt dieser Termin »Abrechnung«.
- Der Termin, zu dem die Bank das Wertpapier zurücknimmt und dem Eigentümer einen vorher vereinbarten Betrag dafür bezahlt. Dieser Termin läuft in den Funktionen unter dem Namen »Fälligkeit«.
Für Ausgabe und Rücknahme derartiger Wertpapiere gibt es mehrere Möglichkeiten:
- Die Papiere werden zum Nennwert verkauft. Anschließend werden für die Laufzeit regelmäßig Zinsen ausgeschüttet (üblich ist ein oder zwei Mal jährlich). Am Ende der Laufzeit wird das Papier zum Nennwert zurückgenommen. Bisweilen wird bei der Ausgabe noch ein Disagio vorgenommen, d. h., vom Nennwert wird ein bestimmter Prozentsatz (eventuell noch orientiert an der Laufzeit) abgezogen.
- Das Papier wird abgezinst verkauft, d. h. zum Nennwert, vermindert um den Betrag, der durch Zinsen während der Laufzeit hinzukommt, und ohne zwischenzeitliche Zinsausschüttungen am Ende der Laufzeit zum Nennwert zurückgenommen.
- Das Papier wird zum Nennwert verkauft und ohne zwischenzeitliche Zinsausschüttungen am Ende der Laufzeit aufgezinst, d. h. zum Nennwert, vermehrt um die aufgelaufenen Zinsen zurückgenommen.
Die Methoden 2. und 3. gelten sinngemäß so auch für unverzinsliche Papiere.
Da derartige Wertpapiere zum Teil auch während der Laufzeit gehandelt werden, stellt sich die Frage nach ihrem Augenblickswert, das ist der Kurs, zu dem sie gehandelt werden können. Dieser Kurs sollte natürlich marktgerecht sein, d. h., ein potenzieller Käufer muss die Möglichkeit haben, zu überprüfen, ob sich die Investition in das betreffende Papier im Vergleich zu anderen möglichen Investitionen lohnt. Hierzu wird als Vergleichsgröße die Rendite eingeführt, also der effektive jährliche Gewinn in Prozent bezogen auf den Kapitaleinsatz. Die Wahl dieser Größe ist auf eine Art willkürlich: Der Kurs wird auf der Grundlage der Rendite berechnet, die mit anderen Anlageformen erzielt werden könnte.
In einer Anzahl von Funktionen taucht das Argument Basis auf. Gemeint ist damit bei Zinsberechnungen die Zeitbasis, auf der gerechnet wird. Die angebotenen Optionen sind:
| 0 | US-amerikanisches System: Die Monate werden mit 30 Tagen, das Jahr mit 360 Tagen gerechnet. |
| 1 | Die tatsächlichen Tage der Monate und die tatsächlichen Tage der Jahre werden gerechnet. |
| 2 | Die tatsächlichen Tage werden gerechnet, das Jahr aber mit 360 Tagen. |
| 3 | Die tatsächlichen Tage werden gerechnet, das Jahr mit 365 Tagen. |
| 4 | Europäisches System: Die Monate werden mit 30 Tagen, das Jahr mit 360 Tagen gerechnet. |
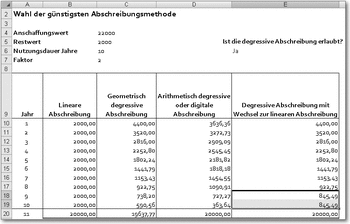
Verkauf eines fest verzinslichen Wertpapiers 
Wenn Sie fest verzinsliche Wertpapiere besitzen und einen Teil davon zu einem bestimmten Termin verkaufen wollen, können Sie sich mit Hilfe der finanzmathematischen Funktionen selbst ausrechnen, was Sie ausgezahlt bekommen. Sie brauchen dazu natürlich die Angabe über den Kurs für den Abrechnungstermin, also den Tag, an dem verkauft werden soll. Aus der Abrechnung beim Kauf der Papiere können Sie die übrigen Daten entnehmen, die nötig sind: das Datum der Emission des Papiers, das Datum der Fälligkeit, den Nominalzinssatz, den Nennwert und die Anzahl der Zinstermine pro Jahr. Aus der Anzahl der Zinstermine ergibt sich der erste Zinstermin.
Excel braucht zusätzlich noch die Angabe über die Basis, auf der die Zinstage berechnet werden. Das ist hier immer der Wert 4, also 360 Tage pro Jahr, 30 Tage pro Monat. In der Zelle C13 wird der aktuelle Kurswert einfach aus Nennwert * Kurs errechnet. Zusätzlich wird noch die Anzahl der Zinstage berechnet. Dafür kann die Formel
=ZINSTERMTAGVA(Abrechnungstermin; Fälligkeit; 1; 4)
verwendet werden. Das Ergebnis dient hier aber nur zur Information, für die Berechnung der inzwischen aufgelaufenen Zinsen wird dieser Wert nicht benötigt.
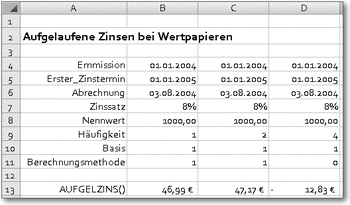
Neben dem Kurs spielt beim Verkauf der Betrag der aufgelaufenen Zinsen eine Rolle. Der kann mit der Funktion AUFGELZINS() berechnet werden. Die Formel lautet:
=AUFGELZINS(Emmission; Erster_Zinstermin; Abrechnungstermin; Zinssatz; Nennwert; Zinstermine_pro_Jahr; Basis_für_Berechnung_der_Zinstage;Berechnungsmethode)
Nun kommen aber noch ein paar Kosten hinzu: Als Provision berechnet die Bank beispielsweise 0,5 % des Nennwerts. Als Maklergebühr kommen noch 0,075 % des Nennwerts hinzu. Dann muss noch eine fixe Spesengebühr entrichtet werden. Der tatsächlich ausgezahlte Betrag ergibt sich dann aus dem Kurswert plus den aufgelaufenen Zinsen, abzüglich der drei genannten Kosten-Posten.
Beachten Sie, dass bei ausländischen Papieren meist etwas andere Maklergebühren berechnet werden.
Verkauf eines fest verzinslichen Wertpapiers
Berechnungen zu Ratenkrediten 
An dieser Stelle werden Ihnen ausnahmsweise zwei zusätzliche Funktionen angeboten. Excel hat zwar einige Funktionen, mit denen sich Annuitätenkredite berechnen lassen, z. B. die RMZ-Funktion zur Berechnung der Rate. Auf die üblichen Ratenkredite für Verbraucher lassen sich diese aber nicht direkt anwenden.
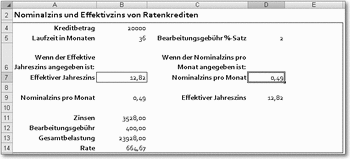
Bei den klassischen Ratenkrediten, wie sie z. B. zur Finanzierung von Möbeln oder Autos benutzt werden, wird in der Regel ein monatlicher Zinssatz angegeben, und die Zinsen werden für jeden Monat vom vollen Kreditbetrag gerechnet. Der Monatszinssatz sieht deshalb meist ziemlich klein aus, beispielsweise aktuell häufig 0,49 %. Die effektive Jahresverzinsung ist aber in diesem Fall keineswegs – wie Sie vielleicht annehmen – 0,49 % * 12 = 5,88 %, sondern in Wirklichkeit 12,82 %, also mehr als das Doppelte.
Die Kreditgeber sind verpflichtet, immer beide Werte, den Monatszins und den effektiven Jahreszins, anzugeben. In der Werbung geschieht das aber beispielsweise nicht immer.
Deshalb hier zwei zusätzliche Funktionen, mit denen jeweils vom angegebenen Monatszins auf den effektiven Jahreszins und vom Jahreszins auf den Monatszins zurückgerechnet werden kann.
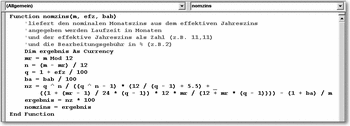
Die Funktion NOMZINS braucht drei Argumente: die Anzahl der Monatsraten, den Effektivzins und den Prozentsatz der Bearbeitungsgebühren.
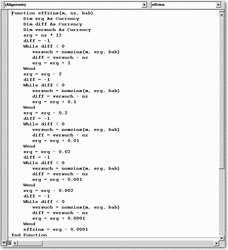
Die Funktion EFFZINS verwendet entsprechend die Argumente Monatsraten, Monatszins und Prozentsatz der Bearbeitungsgebühren. Die Funktion ruft iterativ die NOMZINS-Funktion mehrmals auf, bis ein brauchbares Ergebnis erreicht ist.
Um die Funktionen bequem handhaben zu können, sind die Zellen, die die Argumente liefern, entsprechend benannt worden.
Die folgende Abbildung zeigt die NOMZINS-Funktion.
Die nächste Abbildung zeigt die EFFZINS-Funktion.
Die anderen Berechnungen im Tabellenblatt sind sehr einfach. In Zelle B11 wird die Gesamtsumme der Zinsen berechnet. Die Formel ergibt sich aus dem, was oben gesagt ist:
= Kreditbetrag * Monate * Monatszins
Der Betrag der Bearbeitungsgebühr ist:
= Kreditbetrag * %-Satz der Bearbeitungsgebühr
Die Gesamtbelastung ist die Summe aus Kreditbetrag, Zinsen und Bearbeitungsgebühr. Die Monatsrate kann dann einfach durch Division der Gesamtbelastung durch die Zahl der Monate errechnet werden. In der Praxis werden die Raten allerdings meist auf einen etwas glatteren Betrag gebracht, wobei die erste oder die letzte Rate dann etwas höher oder niedriger ist.
Berechnung eines Ratenkredits
Referenz der finanzmathematischen Funktionen 
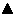
AMORDEGRK()
Syntax: AMORDEGRK(Kosten;Datum;Erste_Periode;Restwert;Periode;
Rate;Basis)Beispiel: AMORDEGRK(10000;"1.7.1997";"31.12.1997";2000;1;0,15;1)Ergebnis: 3045Liefert den Abschreibungsbetrag nach dem französischen Buchhaltungssystem. Die Argumente sind: Kosten der Anschaffung, Datum der Anschaffung, Ende der ersten Periode, Restwert, die Periode, für die der Betrag errechnet werden soll, Abschreibungsrate und Zeitbasis. Die Funktion ist der Funktion AMORLINEARK ähnlich, arbeitet aber zusätzlich mit einem Abschreibungskoeffizienten, der von der Nutzungsdauer abhängig ist.
AMORLINEARK()
Syntax: AMORLINEARK(Kosten;Datum;Erste_Periode;Restwert;
Periode;Rate;Basis)Beispiel: AMORLINEARK(10000;"1.7.1997";"31.12.1997";2000;1;0,15;1)Ergebnis: 1500Liefert den Abschreibungsbetrag nach dem französischen Buchhaltungssystem. Die Argumente sind: Kosten der Anschaffung, Datum der Anschaffung, Ende der ersten Periode, Restwert, die Periode, für die der Betrag errechnet werden soll, Abschreibungsrate und Zeitbasis.
AUFGELZINS()
Syntax: AUFGELZINS(Emission;Erster_Zinstermin;Abrechnung;Zinssatz;
Nennwert;Häufigkeit; Basis;Berechnungsmethode)Beispiel: siehe AbbildungLiefert für Wertpapiere die Summe der aufgelaufenen Zinsen für einen bestimmten Zeitraum bei periodischen Zahlungen. Dient dazu, den Tageswert von fest verzinslichen Papieren zu kalkulieren. Das Verfahren ist in Europa nicht üblich.
Emission ist das Datum der Ausgabe des Wertpapiers (ab diesem Termin wird das Papier verzinst). Erster_Zinstermin ist der Termin, bis zu dem die Verzinsung gültig ist. Mit Abrechnung wird der Stichtag angegeben, für den die aufgelaufenen Zinsen berechnet werden sollen.
Es folgt der Zinssatz des Wertpapiers und der Nennwert (ohne Angabe wird 1 000 angesetzt). Mit Häufigkeit wird angegeben, wie oft die Zinsen im Jahr fällig werden (1, 2 oder 4). Basis gibt an, nach welchem Zeitsystem die Zinstage berechnet werden. Vgl. hierzu die Vorbemerkungen zu den Finanzfunktionen. Berechnungsmethode ist ein Wahrheitswert. 1 bedeutet, dass die insgesamt für alle Zeiträume aufgelaufenen Zinsen ausgegeben werden, 0 bewirkt, dass die Zinsen von Erster_Zinstermin bis zum Abrechnungstermin ausgegeben werden.
Berechnung aufgelaufener Zinsen
AUFGELZINSF()
Syntax: AUFGELZINSF(Emission;Abrechnung;Nominalzins;Nennwert;Basis)Beispiel: siehe Abbildung zu AUFGELZINS()Liefert für Wertpapiere die Summe der aufgelaufenen Zinsen für einen bestimmten Zeitraum bei einmaliger Zahlung zum Abrechnungstermin. Dient dazu, den Tageswert von fest verzinslichen Papieren zu kalkulieren. Das Verfahren ist in Europa nicht üblich.
Emission ist das Datum der Ausgabe des Wertpapiers (ab diesem Termin wird das Papier verzinst). Mit Abrechnung wird der Stichtag angegeben, für den die aufgelaufenen Zinsen berechnet werden sollen.
Nominalzins ist der Zinssatz des Wertpapiers und Nennwert der Nennwert (ohne Angabe wird 1 000 angesetzt). Basis gibt an, nach welchem Zeitsystem die Zinstage berechnet werden. Vgl. hierzu die Vorbemerkungen zu den Finanzfunktionen.
AUSZAHLUNG()
Syntax: AUSZAHLUNG(Abrechnung;Fälligkeit;Anlage;Disagio;Basis)Beispiel: AUSZAHLUNG(DATWERT("25.02.94");DATWERT("30.06.94");
10000;3,5 %;0)Ergebnis: 10123,02Liefert den Auszahlungsbetrag, den Sie für eine Anlage in fest verzinslichen Wertpapieren zu einem bestimmten Zeitpunkt erhalten.
Mit Abrechnung wird der Zeitpunkt des Kaufs angegeben, mit Fälligkeit der Zeitpunkt, zu dem der Auszahlungsbetrag berechnet werden soll. Anlage ist die Summe, die beim Kauf investiert wird. (Die Funktion setzt voraus, dass der Gesamtbetrag in die Wertpapiere investiert wird.) Disagio ist der prozentuale Abschlag, den Sie bei der Ausgabe erhalten (bei 5 % Disagio z. B. wird ein Wertpapier mit einem Nominalwert von 100 EURO für 95 EURO verkauft). Basis gibt an, nach welchem Zeitsystem die Zinstage berechnet werden. Vgl. hierzu die Vorbemerkungen zu den Finanzfunktionen.
BW()
Syntax: BW(Zins;Zzr;Rmz;Zw;F)Beispiel: =BW(0,08;20;10000;;0)Ergebnis: -98.181,47 EURO (um 20 Jahre lang jedes Jahr 10 000 EURO zu erhalten,
müsste ich heute 98.181,47 EURO bei 8 % Zinsen auf der Bank einzahlen).
Die Funktion berechnet den Barwert einer Reihe von regelmäßigen Zahlungen.
Mit Zins wird der Zins und mit Zzr die Zahlungszeiträume (oder die Anzahl der Zahlungen) angegeben.
Außer dem Betrag, der periodisch zu zahlen ist (Rmz oder auch die Ratenzahlung), können noch zwei optionale Argumente angegeben werden. Zw bedeutet den Zukunftswert, der nach der letzten Zahlung erreicht werden soll (im obigen Beispiel, wie viel Geld nach 20 Jahren auf der Bank übrig sein soll). Wird Zw nicht angegeben, so wird er als 0 angenommen.
Mit F wird angegeben, ob die Zahlungen jeweils am Ende einer Periode erfolgen (F = 0 oder weggelassen) oder am Anfang (F = 1).
Grundlage der Funktion BW() ist die Formel
Barwert = Rate*(q^Zzr-1)/((q^Zzr)*(q-1))
wobei mit q der Zinsfaktor gemeint ist (q = 1+(Zins/100)).
DIA()
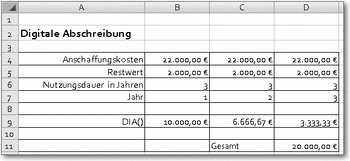
Syntax: DIA(Ansch_Wert;Restwert;Nutzungsdauer;Zr)Beispiel: DIA(20000;3500;10;4)Ergebnis: 2100Die Funktion berechnet die Abschreibungsrate für einen bestimmten Abschreibungszeitraum nach der digitalen Methode.
Das Argument Ansch_Wert ist der Betrag, der für die Investition aufgewandt wurde. Restwert ist der Wert, den die Investition nach der Abschreibung noch hat. Nutzungsdauer entspricht der Anzahl von Zeiträumen bis zum Ende der Abschreibung. Zr ist der Zeitraum, für den die Abschreibung errechnet werden soll.
Digitale Abschreibung
DISAGIO()
Syntax: DISAGIO(Abrechnung;Fälligkeit;Kurs;Rückzahlung;Basis)Beispiel: DISAGIO(DATWERT("02.02.94");DATWERT("06.08.94");96;100)Ergebnis: 7,83 %Berechnet das Disagio (Abschlag beim Handel mit einem Wertpapier).
Abrechnung ist der Kauf- bzw. Emissionstermin, Fälligkeit der Termin des Verkaufs. Kurs ist der Wert zum Kauftermin und Rückzahlung der Wert zum Verkaufstermin. Basis gibt an, nach welchem Zeitsystem die Zinstage berechnet werden. Vgl. hierzu die Vorbemerkungen zu den Finanzfunktionen.
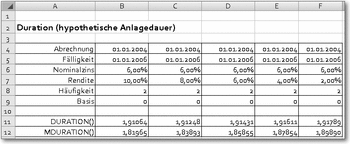
DURATION()
Syntax: DURATION(Abrechnung;Fälligkeit;Nominalzins;Rendite;
Häufigkeit;Basis)Beispiel: siehe AbbildungLiefert die hypothetische Anlagedauer eines fest verzinslichen Wertpapiers in Jahren.
Je niedriger die hypothetische Anlagedauer im Vergleich zur tatsächlichen ist, umso profitabler ist das Wertpapier.
Abrechnung ist der Kauf- oder Emissionstermin, Fälligkeit der Verkaufstermin. Mit Nominalzins wird der Zinssatz angegeben, mit Rendite der tatsächlich erzielte Zinssatz (setzt sich zusammen aus dem Nominalzins und dem Gewinn aus der Differenz von Kauf- und Verkaufspreis). Häufigkeit ist die Zahl der Zinszahlungen im Jahr (1, 2, oder 4). Basis gibt an, nach welchem Zeitsystem die Zinstage berechnet werden. Vgl. hierzu die Vorbemerkungen zu den Finanzfunktionen.
Hypothetische Anlagedauer
EFFEKTIV()
Syntax: EFFEKTIV(Nominalzins;Perioden)Beispiel: EFFEKTIV(8 %;12)Ergebnis: 8,3 %Liefert den effektiven Jahreszins für eine Anlage oder ein Darlehen.
Nominalzins ist der jährliche Nominalzins, Perioden die Zahl der jährlichen Zinszahlungen.
Da bei mehreren jährlichen anteiligen Zinszahlen ein Teil der Jahreszinsen praktisch vorweg gezahlt wird, erhöht sich der Effektivzins mit der Zahl der jährlichen Zinszahlungen.
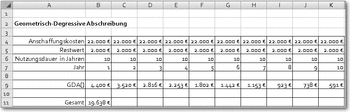
GDA()
Syntax: GDA(Ansch_Wert;Restwert;Nutzungsdauer;Periode;Faktor)Beispiel: GDA(30000;3000;8;3)Ergebnis: 4218,75 EURODie Funktion berechnet die Abschreibungsrate für einen bestimmten Abschreibungszeitraum nach der geometrisch-degressiven Methode.
Das Argument Ansch_Wert ist der Betrag, der für die Investition aufgewandt wurde. Restwert ist der Wert, den die Investition nach der Abschreibung noch hat. Nutzungsdauer entspricht der Anzahl von Zeiträumen bis zum Ende der Abschreibung. Periode ist der Zeitraum, für den die Abschreibung ermittelt werden soll. Mit Faktor wird die Stärke der Degressivität angegeben (ohne Angabe wird 2 angesetzt).
Der Buchwert kann mit dieser Methode nie auf 0 gehen, deshalb wird in der Praxis für spätere Perioden auf die lineare Abschreibung übergegangen.
Geometrisch-degressive Abschreibung
GDA2()
Syntax: GDA2(Ansch_Wert;Restwert;Nutzungsdauer;Periode;Monate)Beispiel: GDA2(30000;3000;8;3;6)Ergebnis: 4921,88Die Funktion berechnet die Abschreibungsrate für einen bestimmten Abschreibungszeitraum nach der geometrisch-degressiven Methode (vgl. GDA).
Das Argument Ansch_Wert ist der Betrag, der für die Investition aufgewandt wurde. Restwert ist der Wert, den die Investition nach der Abschreibung noch hat. Nutzungsdauer entspricht der Anzahl von Zeiträumen bis zum Ende der Abschreibung. Periode ist der Zeitraum, für den der Abschreibungsbetrag ermittelt werden soll. Wird das optionale Argument Monate weggelassen, so wird es von Excel als 12 angenommen. Die Funktion liefert dann denselben Wert wie GDA(). Tragen Sie für Monate einen anderen Wert als 12 ein, so wird die Abschreibung für die Anzahl der Monate im entsprechenden Jahr berechnet.
IKV()
Syntax: IKV(Werte;Schätzwert)Beispiel: IKV(A1:A6) für A1:A6 –20000; 8000; 6000; 5000; 5500; 3000Ergebnis: 14 %Die Funktion berechnet den internen Ertragszins einer Investition. Dadurch kann die Rentabilität einer Investition geprüft werden.
Das Argument Werte ist eine Matrix oder ein Bereich, der mindestens einen positiven und einen negativen Wert enthält. Der erste Wert stellt die getätigte Investition als Ausgabe dar, erscheint also negativ, die weiteren Zellen stellen die periodischen Rückflüsse dar.
Das optionale Argument Schätzwert sollte mit einem Wert belegt werden, der in einer Schätzung dem erwarteten Ergebnis schon möglichst nahe kommt. Wird er nicht eingetragen, so wird sein Wert von Excel mit 10 % angenommen.
ISPMT()
Syntax: ISPMT(Zins;Zr;Zzr;Bw)Beispiel: ISPMT(0,08;3;8;50000)Ergebnis: -2500Berechnet die Zinsen, die während einer bestimmten Periode gezahlt werden.
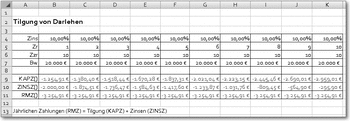
KAPZ()
Syntax: KAPZ(Zins;Zr;Zzr;Bw;Zw;F)Beispiel: KAPZ(0,08;3;8;50000;;)Ergebnis: -5482,94 EURODie Funktion berechnet den Tilgungsanteil für die Abzahlung eines Darlehens.
Das Darlehen wird in periodischen, gleich bleibenden Raten abbezahlt, deren Höhe mit RMZ() berechnet wird. Die Raten bestehen jeweils aus einem Zinsanteil (berechnet mit ZINSZ) und einem Tilgungsanteil, um den sich die Gesamtschuld jeweils verringert.
Tilgung von Darlehen
Argumente sind Zins (der konstante Zinssatz), Zr (der Zeitraum, für den die Zahlung berechnet werden soll), Zzr (die Anzahl der Abzahlungszeiträume) und Bw (der Barwert, bei einem Darlehen der Auszahlungsbetrag).
Als optionalen Wert außer F (Fälligkeit; 0 = nachschüssig, 1 = vorschüssig) können Sie noch Zw angeben (den Zukunftswert oder den Betrag, der am Ende der letzten Zahlung vorhanden sein soll).
KUMKAPITAL()
Syntax: KUMKAPITAL(Zins;Zzr;Bw;Zeitraum_Anfang;Zeitraum_Ende;F)Beispiel: KUMKAPITAL(6 %;12;10000;1;2;0)Ergebnis: -1221,11Berechnet den Betrag, der für die Tilgung eines Darlehens in einem bestimmten Zeitraum aufgebracht wird (nicht zu verwechseln mit den Zahlungsbeträgen).
Mit Zins wird der Zinssatz pro Zinszeitraum angegeben; mit Zzr die Anzahl der Zahlungsperioden, mit Bw der Barwert (ausgegebener Betrag) des Darlehens. Zeitraum_Anfang und Zeitraum_Ende sind die Nummern der beiden Zahlungsperioden, zwischen denen die Gesamttilgung berechnet werden soll. Mit F lässt sich angeben, ob die Zahlungen vorschüssig (1) oder nachschüssig (0 oder weggelassen) erfolgen sollen.
Während mit KUMKAPITAL der Tilgungsanteil berechnet wird, liefert die folgende Funktion KUMZINSZ den Zinsanteil für den betreffenden Zeitraum. Beides zusammen ist der Betrag, der für den betreffenden Zeitraum insgesamt aufgebracht werden muss.
Analog verhalten sich die Funktionen KAPZ() und ZINSZ(), beide zusammen ergeben die RMZ().
KUMZINSZ()
Syntax: KUMZINSZ(Zins;Zzr;Bw;Zeitraum_Anfang;Zeitraum_Ende;F)Beispiel: KUMZINSZ(6 %;12;10000;1;1;0)Ergebnis: -600Berechnet den Betrag, der für die Zinsen eines Darlehens in einem bestimmten Zeitraum aufgebracht wird (nicht zu verwechseln mit den Zahlungsbeträgen).
Die Argumente der Funktion sind identisch mit denen von KUMKAPITAL (siehe dort, an dieser Stelle wird auch das Verhältnis der beiden Funktionen zueinander dargelegt).
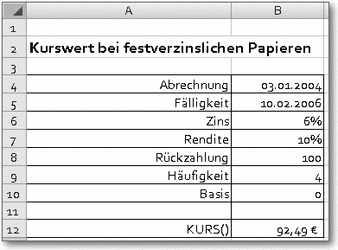
KURS()
Syntax: KURS(Abrechnung;Fälligkeit;Zins;Rendite;Rückzahlung;
Häufigkeit;Basis)Beispiel: siehe AbbildungLiefert den Kurswert eines fest verzinslichen Wertpapiers mit dem Nennwert 100 EURO abhängig von der anvisierten Rendite.
Abrechnung ist das Verkaufsdatum; Fälligkeit das Fälligkeitsdatum des Wertpapiers. Mit Zins wird der Nominalzins angegeben, mit Rendite die Rendite, die das Papier bringen soll. Rückzahlung ist der Betrag, zu dem das Wertpapier zum Fälligkeitstermin ausbezahlt wird (bei Anleihen im Allgemeinen 100). Häufigkeit gibt an, wie oft die Zinsen im Jahr ausgeschüttet werden. Basis gibt an, nach welchem Zeitsystem die Zinstage berechnet werden. Vgl. hierzu die Vorbemerkungen zu den Finanzfunktionen.
Kurswert von fest verzinslichen Papieren
KURSDISAGIO()
Syntax: KURSDISAGIO(Abrechnung;Fälligkeit;Disagio;Rückzahlung;Basis)Beispiel: KURSDISAGIO(DATWERT("1.3.94");DATWERT("2.10.96");2 %;
100;0)Ergebnis: 94,83Berechnet den Ausgabekurs eines nicht verzinslichen Wertpapiers mit einem Nennwert von 100 EURO.
Abrechnung ist der Ausgabetermin, Fälligkeit der Rücknahmetermin. Rückzahlung ist der Wert des Papiers zum Fälligkeitstermin. Disagio legt fest, mit welchem Abschlag (aufs Jahr gerechnet) das Papier verkauft werden soll. Basis gibt an, nach welchem Zeitsystem die Zinstage berechnet werden. Vgl. hierzu die Vorbemerkungen zu den Finanzfunktionen.
KURSFÄLLIG()
Syntax: KURSFÄLLIG(Abrechnung;Fälligkeit;Emission;Zins;Rendite;Basis)Beispiel: KURSFÄLLIG(DATWERT("6.5.94");DATWERT("31.12.98"); DATWERT("1.1.93");7,5 %;6 %;0)Ergebnis: 103,25Liefert den Kurswert eines fest verzinslichen Wertpapiers (Nennwert 100 EURO), bei dem die Zinsen zum Fälligkeitsdatum (mit der Rückzahlung) ausgezahlt werden.
Abrechnung ist das Datum, zu dem der Kurswert errechnet werden soll, Fälligkeit das Datum, zu dem das Wertpapier zurückgenommen wird. Emission ist das Ausgabedatum, ab dem die Zinsen laufen; Zins der jährliche Zins.
Mit Rendite wird angegeben, wie viel das Wertpapier jährlich einbringen soll (in Prozent vom Kaufpreis). Basis gibt an, nach welchem Zeitsystem die Zinstage berechnet werden. Vgl. hierzu die Vorbemerkungen zu den Finanzfunktionen.
LIA()
Syntax: LIA(Ansch_Wert;Restwert;Nutzungsdauer)Beispiel: LIA(12000;2000;8)Ergebnis: 1250 EURODie Funktion berechnet die Abschreibungsrate für einen bestimmten Abschreibungszeitraum nach der linearen Methode (AFA).
Bei dieser Methode wird über den gesamten Abschreibungszeitraum mit periodisch gleich bleibenden Beträgen abgeschrieben.
Das Argument Ansch_Wert ist der Betrag, der für die Investition aufgewandt wurde. Restwert ist der Wert, den die Investition nach der Abschreibung noch hat. Nutzungsdauer entspricht der Anzahl von Zeiträumen bis zum Ende der Abschreibung.
Lineare Abschreibung
MDURATION()
Syntax: MDURATION(Abrechnung;Fälligkeit;Nominalzins;Rendite;
Häufigkeit;Basis)Beispiel: siehe Abbildung zu DURATION()Liefert die modifizierte Duration (liefert eine deutlichere Aussage als die Funktion DURATION).
Zu den Argumenten vgl. DURATION.
NBW()
Syntax: NBW(Zins;Wert1;Wert2;...)Beispiel: NBW(0,09;-12000;4000;4000;6000)Ergebnis: -303,17Die Funktion berechnet den Nettokapitalwert periodischer Cashflow (Ein- oder Auszahlungen).
Mit Zins wird ein konstanter Zinssatz für den gesamten betrachteten Zeitraum angegeben. Wert1, Wert2, ... sind Zahlungen (Einzahlung positiv, Auszahlung negativ), die jeweils am Ende einer Periode erfolgen.
Ist das Ergebnis negativ, dann wäre es besser gewesen, das Geld zum angegebenen Zinssatz auf die Bank zu tragen.
NOMINAL()
Syntax: NOMINAL(Effektiver_Zins;Perioden)Beispiel: NOMINAL(6,3 %;4)Ergebnis: 6,16 %Berechnet den Nominalzins (Jahreszins auf den Nennwert). Die Funktion ist die Umkehrung der Funktion EFFEKTIV().
Mit Effektiver_Zins wird der tatsächlich erzielte Jahreszins angegeben; Perioden ist die Zahl der jährlichen Zinszahlungen. Bei einer jährlichen Zahlung sind Nominalzins und Effektivzins identisch.
NOTIERUNGBRU()
Syntax: NOTIERUNGBRU(Zahl;Teiler)Beispiel: NOTIERUNGBRU(1,2;5)Ergebnis: 1,1Liefert einen als Bruch interpretierbaren Ausdruck einer Dezimalzahl.
Zahl ist die umzuwandelnde Zahl; Teiler der Nenner des Bruchs. Ist der Teiler wie im Beispiel 5, dann ist die Nachkommastelle des Ergebnisses zu lesen als 1/5.
NOTIERUNGDEZ()
Syntax: NOTIERUNGDEZ(Zahl;Teiler)Beispiel: NOTIERUNGDEZ(1,1;5)Ergebnis: 1,2Konvertiert einen als Bruch interpretierten Ausdruck (ZAHL) in eine Dezimalzahl. Die Funktion ist die Umkehrung zu NOTIERUNGBRU() (siehe dort).
QIKV()
Syntax: QIKV(Werte;Investition;Reinvestition)Beispiel: QIKV(A1:A5;8 %;11 %) (für A1:A5 –85000; 21000; 24000; 28000; 35000)Ergebnis: 9,98 %Mit dieser Funktion bestimmen Sie die interne Ertragsrate einer Reihe von Cashflows (Ein- und Auszahlungen).
Drei Argumente müssen für die Funktion eingetragen werden:
Werte ist ein Bezug oder eine Reihe von Zellen, die die Werte von Abgängen und Eingängen enthalten. Es müssen mindestens ein negativer und ein positiver Wert vorhanden sein (positiv für Eingänge); der erste Betrag wird zumeist der Investition entsprechen und somit ein negativer Wert sein.
Investition ist der Zinssatz für die Einzahlungen; Reinvestition ist der Zinssatz für reinvestierte Beträge.
RENDITE()
Syntax: RENDITE(Abrechnung;Fälligkeit;Zins;Kurs;Rückzahlung;
Häufigkeit;Basis)Beispiel: RENDITE(DATWERT("3.4.94");DATWERT("1.6.98");5 %;96;
100;4;0)Ergebnis: 6,095 %Berechnet die jährliche Rendite eines fest verzinslichen Wertpapiers.
Abrechnung ist der Kauftermin, Fälligkeit der Rücknahme- und damit Auszahlungstermin. Zins ist der Nominalzins. Das Papier wurde zum Preis von Kurs erworben und wird zum Fälligkeitstermin zum Preis von Rückzahlung eingelöst. Häufigkeit ist die Anzahl der jährlichen Zinsausschüttungen. Basis gibt an, nach welchem Zeitsystem die Zinstage berechnet werden. Vgl. hierzu die Vorbemerkungen zu den Finanzfunktionen.
Liefert die Rendite eines Wertpapiers, das periodisch Zinsen auszahlt. Mit RENDITE können Sie die Rendite von Anleihen und Obligationen berechnen.
RENDITEDIS()
Syntax: RENDITEDIS(Abrechnung;Fälligkeit;Kurs;Rückzahlung;Basis)Beispiel: RENDITEDIS(DATWERT("3.4.94";"1.6.98";78;100;0)Ergebnis: 6,78 %Berechnet die jährliche Rendite eines unverzinslichen Wertpapiers.
Zur Interpretation der Argumente vgl. RENDITE().
RENDITEFÄLL()
Syntax: RENDITEFÄLL(Abrechnung;Fälligkeit;Emission;Zins;Kurs;Basis)Beispiel: RENDITEFÄLL(DATWERT("3.4.94);DATWER("1.6.98"); DATWERT("1.6.88");5 %;96;0)Ergebnis: 4,76 %Berechnet die jährliche Rendite eines fest verzinslichen Wertpapiers, dessen Zinsen zusammen mit der Rückzahlung zum Fälligkeitstermin ausgezahlt werden.
Abrechnung ist der Kauftermin, Fälligkeit der Rücknahme- und damit Auszahlungstermin, Emission der Ausgabetermin, ab dem die Verzinsung läuft. Zins ist der Nominalzins. Das Papier wurde zum Preis von Kurs am Abrechnungstermin erworben und wird zum Fälligkeitstermin zum Preis von Rückzahlung zusammen mit den aufgelaufenen Zinsen eingelöst. Basis gibt an, nach welchem Zeitsystem die Zinstage berechnet werden. Vgl. hierzu die Vorbemerkungen zu den Finanzfunktionen.
RMZ()
Syntax: RMZ(Zins;Zzr;Bw;Zw;F)Beispiel: RMZ(0,09/12;8;8000)Ergebnis: -1034,04 EURODie Funktion liefert die kontinuierlichen Raten für eine Investition. Argumente sind Zins, Zzr (die Zahlungszeiträume) und Bw (der Barwert, die Investition). Optional kann außer F (Fälligkeit; 0 für Ende der Perioden, 1 für Anfang) noch Zw (Zukunftswert) eingegeben werden. Vgl. KAPZ().
TBILLÄQUIV()
Syntax: TBILLÄQUIV(Abrechnung;Fälligkeit;Disagio)Beispiel: TBILLÄQUIV(DATWERT("3.4.94");DATWERT("12.10.94");8 %)Ergebnis: 8,45 %Berechnet die jährliche Verzinsung eines Schatzwechsels (Treasury Bill).
Ein Schatzwechsel ist eine kurzfristige Schuldverschreibung, die zum Termin Abrechnung mit einem Abschlag von Disagio (in Prozent auf ein Jahr umgerechnet) erworben wird und zum Termin Fälligkeit zum vollen Wert eingelöst wird. Abrechnung und Fälligkeit müssen im gleichen Jahr liegen.
Da der Disagio praktisch ein vorschüssiger Zins ist, rechnet die Funktion um, wie der Disagio sich in einem nachschüssigen Zins widerspiegeln würde.
TBILLKURS()
Syntax: TBILLKURS(Abrechnung;Fälligkeit;Disagio)Beispiel: TBILLKURS(DATWERT("3.4.94");DATWERT("12.10.94");8 %)Ergebnis: 95,73Liefert den Ausgabekurs für einen Schatzwechsel, der einen Nominalwert (und damit Rückgabewert) von 100 EURO hat.
Zu den Argumenten vgl. TBILLÄQUIV().
TBILLRENDITE()
Syntax: TBILLRENDITE(Abrechnung;Fälligkeit;Kurs)Beispiel: TBILLRENDITE(DATWERT("3.4.94");DATWERT("12.10.94");95)Ergebnis: 9,87 %Liefert die Rendite eines Schatzwechsels, der zu einem Ausgabekurs von Kurs erworben wurde.
Zu den Argumenten vgl. TBILLÄQUIV().
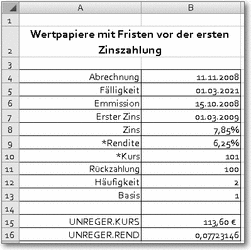
UNREGER.KURS()
Syntax: UNREGER.KURS(Abrechnung;Fälligkeit;Emission;Erster_Zinstermin;
Zins;Rendite; Rückzahlung;Häufigkeit;Basis)Beispiel: siehe AbbildungLiefert den Kurswert eines fest verzinslichen Wertpapiers (Nennwert 100 EURO), bei dem die Zinsausschüttungen erst nach einer bestimmten Frist einsetzen und von da an regelmäßig erfolgen.
Abrechnung ist der Verkaufstermin, für den der Kurs errechnet werden soll, Fälligkeit der Rückzahlungstermin. Emission ist der Ausgabetermin, ab dem die Zinsberechnung läuft. Der Termin, ab dem die Zinszahlungen einsetzen, wird mit Erster_Zinstermin angegeben, der Nominalzins mit Zins.
Kurs und Rendite bei Papieren mit verzögerter erster Zinsausschüttung
Rendite ist die anvisierte Rendite des Papiers; Rückzahlung der Betrag, der zum Fälligkeitstermin ausbezahlt wird. Häufigkeit gibt an, wie oft im Jahr die Zinsen ausgeschüttet werden (1, 2 oder 4). Basis gibt an, nach welchem Zeitsystem die Zinstage berechnet werden. Vgl. hierzu die Vorbemerkungen zu den Finanzfunktionen.
Das mit * bezeichnete Argument Kurs wird bei der folgenden Funktion UNREGER.REND benötigt; das Argument Rendite bei der vorliegenden Funktion UNREGER.KURS.
UNREGER.REND()
Syntax: UNREGER.REND(Abrechnung;Fälligkeit;Emission;Erster_Zinstermin;Zins;Kurs;Rückzahlung;Häufigkeit;Basis)Beispiel: siehe Abbildung zu UNREGER.KURSLiefert die Rendite eines fest verzinslichen Wertpapiers (Nennwert 100 EURO), bei dem die Zinsausschüttungen erst nach einer bestimmten Frist einsetzen und von da an regelmäßig erfolgen.
Kurs ist der Wert des Wertpapiers zum Abrechnungstermin. Zu den übrigen Argumenten vgl. UNREGER.KURS.
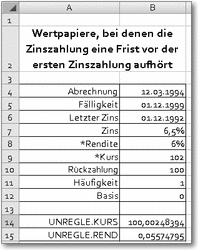
UNREGLE.KURS()
Syntax: UNREGLE.KURS(Abrechnung;Fälligkeit;Letzter_Zinstermin;Zins;
Rendite;Rückzahlung;Häufigkeit;Basis)Beispiel: siehe AbbildungLiefert den Kurswert eines fest verzinslichen Wertpapiers (Nennwert 100 EURO), bei dem die bis dahin regelmäßigen Zinsausschüttungen eine bestimmte Frist vor dem Fälligkeitstermin aussetzen.
Abrechnung ist der Verkaufstermin, für den der Kurs errechnet werden soll, Fälligkeit der Rückzahlungstermin. Letzter_Zinstermin ist der letzte Termin vor Abrechnung, zu dem noch Zinsen bezahlt werden. Der Nominalzins wird mit Zins angegeben.
Rendite ist die anvisierte Rendite des Papiers, Rückzahlung der Betrag, der zum Fälligkeitstermin ausbezahlt wird. Häufigkeit gibt an, wie oft im Jahr die Zinsen ausgeschüttet werden (1, 2 oder 4). Basis gibt an, nach welchem Zeitsystem die Zinstage berechnet werden. Vgl. hierzu die Vorbemerkungen zu den Finanzfunktionen.
Die angegebenen Termine müssen so liegen, dass in zeitlicher Reihenfolge Letzter_Zinstermin vor Abrechnung und dies vor Fälligkeit kommt. Andernfalls gibt die Funktion eine Fehlermeldung aus.
Von den Argumenten wird *Kurs nur für die folgende Funktion UNREGLE.REND() benötigt, bei der dann naturgemäß *Rendite wegfällt.
Kurs und Rendite für Wertpapiere mit begrenzter Zinsausschüttung
UNREGLE.REND()
Syntax: UNREGLE.REND(Abrechnung;Fälligkeit;Letzter_Zinstermin;Zins;Kurs;
Rückzahlung; Häufigkeit;Basis)Beispiel: siehe Abbildung zu UNREGLE.KURSLiefert die Rendite eines fest verzinslichen Wertpapiers (Nennwert 100 EURO), bei dem die bis dahin regelmäßigen Zinsausschüttungen eine bestimmte Frist vor dem Fälligkeitstermin aussetzen. Das Papier wird nach dem letzten Zinstermin und vor der Fälligkeit zum Preis von Kurs verkauft.
Zu den Argumenten vgl. UNREGLE.KURS.
VDB()
Syntax: VDB(Ansch_Wert;Restwert;Nutzungsdauer;Anfang;Ende;Faktor;
Nicht_wechseln)Beispiel: VDB(30000;2000;7;0;1)Ergebnis: 4000Die Funktion berechnet die Abschreibungsrate für einen bestimmten Abschreibungszeitraum nach der variabel-degressiven Methode.
Diese Funktion ist eine Variation der geometrisch-degressiven Abschreibung. Sie ermöglicht es, sobald die lineare Abschreibung höhere Abschreibungsbeträge liefert, in diese überzuwechseln.
Das Argument Ansch_Wert ist der Betrag, der für die Investition aufgewandt wurde. Restwert ist der Wert, den die Investition nach der Abschreibung noch hat. Nutzungsdauer entspricht der Anzahl von Zeiträumen bis zum Ende der Abschreibung. Mit Faktor wird die Stärke der Degressivität angegeben (ohne Angabe wird 2 angesetzt).
Anfang ist der Anfang der Periode, für die die Abschreibung berechnet werden soll, Ende der Endzeitpunkt. Soll z. B. die Abschreibung für das erste Jahr berechnet werden, dann wären 0 und 1 einzusetzen. Die Abschreibung kann so auch über mehrere Perioden berechnet werden.
Nicht_wechseln wird durch einen Wahrheitswert geschaltet. Wenn die nach der linearen Methode erzielten Abschreibungen höher liegen als bei der degressiven, wechselt die Funktion auf die lineare Abschreibung, falls Nicht_wechseln mit FALSCH belegt wird oder nicht angegeben ist. Ist das Argument mit WAHR belegt, so wird das Abschreibungsverfahren nicht geändert.
Variable Abschreibung
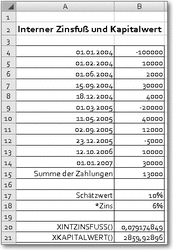
XINTZINSFUSS()
Syntax: XINTZINSFUSS(Werte;Zeitpkte;Schätzwert)Beispiel: siehe AbbildungBerechnet den internen Zinsfuß für eine Reihe von Zahlungen, die in unterschiedlicher Höhe zu nicht regelmäßigen Zeitpunkten erfolgen werden.
Mit dieser Funktion lassen sich auch Investitionen und Cashflow, die sonst sehr undurchschaubar bleiben, überprüfen.
Werte sind die Zahlungen, die erfolgen, wobei mindestens ein positiver und ein negativer Wert enthalten sein müssen. Zeitpkte sind die zu den Zahlungen gehörenden Zeitpunkte. Der erste Zeitpunkt ist der Beginn des Zahlungsplans, alle anderen müssen später liegen, brauchen aber nicht unbedingt in zeitlicher Reihenfolge angeordnet zu sein. Mit Schätzwert kann eine Vorgabe für den erwarteten internen Zinsfuß gemacht werden, ohne Angabe geht Excel von 10 % aus.
Interner Zinsfuß und Kapitalwert bei unregelmäßigen Zahlungen
Das Argument *Zins wird bei der folgenden Funktion XKAPITALWERT benötigt.
XKAPITALWERT()
Syntax: XKAPITALWERT(Zins;Werte;Zeitpkte)Beispiel: siehe Abbildung zu XINTZINSFUSS()Berechnet den Nettokapitalwert für eine Reihe von Zahlungen, die in unterschiedlicher Höhe zu nicht regelmäßigen Zeitpunkten erfolgen werden.
Mit dieser Funktion lassen sich auch Investitionen und Cashflow, die sonst sehr undurchschaubar bleiben, überprüfen.
Zu den Argumenten vgl. XINTZINSFUSS().
ZINS()
Syntax: ZINS(Zzr;Rmz;Bw;Zw;F;Schätzwert)Beispiel: ZINS(8;-11000;60000)Ergebnis: 9 %Die Funktion berechnet den Zinssatz einer Investition bei regelmäßigen Auszahlungen.
Zzr sind die Zahlungszeiträume, über die die Auszahlungen erfolgen. Rmz ist der über die Zahlungszeiträume konstante regelmäßige Auszahlungsbetrag (muss negativ sein). Bw der Barwert, also der aktuelle Wert, z. B. die anfängliche Einzahlung.
Wird Zw (der Zukunftswert) nicht angegeben, so wird er von der Funktion als 0 angenommen, wird F (Zahlungen am Anfang oder am Ende der Zahlungszeiträume) nicht gesetzt, so wird es ebenfalls als 0 (Ende der Periode) angenommen.
Mit Schätzwert können Sie angeben, wie hoch Sie den Zins einschätzen (das kann das Rechenverfahren verkürzen). Geben Sie keinen Wert ein, so wird er von der Funktion mit 10 % veranschlagt.
ZINSSATZ()
Syntax: ZINSSATZ(Abrechnung;Fälligkeit;Anlage;Rückzahlung;Basis)Beispiel: ZINSSATZ(DATWERT("1.4.94");DATWERT("19.9.94");12000;
12600;0)Ergebnis: 10,71 %Berechnet den (jährlichen) Zinssatz für eine Investition, bei der zwischen Abrechnung und Rückzahlung keine Zinsen ausgeschüttet werden.
Bei der Investition handelt es sich nach der Terminologie der Argumente um den Kauf von Wertpapieren, die Funktion kann aber auf jede Situation angewendet werden, in der ein Betrag eingezahlt und ein anderer Betrag nach einer Frist zurückgezahlt wird.
Abrechnung ist der Kauftermin, Fälligkeit der Rücknahmetermin. Anlage ist der Betrag, der angelegt wurde, Rückzahlung der Betrag, der zum Fälligkeitstermin zurückgezahlt wird. Basis gibt an, nach welchem Zeitsystem die Zinstage berechnet werden. Vgl. hierzu die Vorbemerkungen zu den Finanzfunktionen.
ZINSTERMNZ()
Syntax: ZINSTERMNZ(Abrechnung;Fälligkeit;Häufigkeit;Basis)Beispiel: ZINSTERMNZ(DATWERT("1.4.94");DATWERT("19.9.94");4;0)Ergebnis: 19.06.1994Berechnet das Datum der ersten Zinsausschüttung nach dem Kauftermin (Abrechnung).
Abrechnung ist der Kauftermin, Fälligkeit der Rücknahmetermin. Häufigkeit ist die Zahl der jährlichen Zinsausschüttungen (1, 2 oder 4). Basis gibt an, nach welchem Zeitsystem die Zinstage berechnet werden. Vgl. hierzu die Vorbemerkungen zu den Finanzfunktionen.
ZINSTERMTAGE()
Syntax: ZINSTERMTAGE(Abrechnung;Fälligkeit;Häufigkeit;Basis)Beispiel: ZINSTERMTAGE(DATWERT("1.5.94");DATWERT("19.9.94");4;3)Ergebnis: 92Berechnet die Anzahl der Tage in derjenigen Zinsperiode, in die der Abrechnungszeitpunkt fällt.
Abrechnung ist der Kauftermin, Fälligkeit der Rücknahmetermin. Häufigkeit ist die Zahl der jährlichen Zinsausschüttungen (1, 2 oder 4). Basis gibt an, nach welchem Zeitsystem die Zinstage berechnet werden. Vgl. hierzu die Vorbemerkungen zu den Finanzfunktionen.
Die Funktion hat natürlich nur Sinn, wenn die Basis so gewählt ist, dass das Zinsjahr nicht mit 360 Tagen gerechnet wird (sonst kommt bei einer Häufigkeit von 4 immer 90 heraus) und wenn die Häufigkeit nicht mit 1 angesetzt ist (sonst kommt immer 360 bzw. 365 heraus).
ZINSTERMTAGNZ()
Syntax: ZINSTERMTAGNZ(Abrechnung;Fälligkeit;Häufigkeit;Basis)Beispiel: ZINSTERMTAGNZ(DATWERT("1.5.94");DATWERT("19.9.94");4;3)Ergebnis: 49Berechnet die Tage vom Kauftermin bis zum ersten Zinstermin.
Abrechnung ist der Kauftermin, Fälligkeit der Rücknahmetermin. Häufigkeit ist die Zahl der jährlichen Zinsausschüttungen (1, 2 oder 4). Basis gibt an, nach welchem Zeitsystem die Zinstage berechnet werden. Vgl. hierzu die Vorbemerkungen zu den Finanzfunktionen.
ZINSTERMTAGVA()
Syntax: ZINSTERMTAGVA(Abrechnung;Fälligkeit;Häufigkeit;Basis)Beispiel: ZINSTERMTAGVA(DATWERT("1.5.94");DATWERT("19.9.94");4;3)Ergebnis: 43Berechnet die Tage vom letzten Zinstermin vor der Abrechnung bis zur Abrechnung.
Abrechnung ist der Kauftermin, Fälligkeit der Rücknahmetermin. Häufigkeit ist die Zahl der jährlichen Zinsausschüttungen (1, 2 oder 4). Basis gibt an, nach welchem Zeitsystem die Zinstage berechnet werden. Vgl. hierzu die Vorbemerkungen zu den Finanzfunktionen.
ZINSTERMVZ()
Syntax: ZINSTERMVZ(Abrechnung;Fälligkeit;Häufigkeit;Basis)Beispiel: ZINSTERMVZ(DATWERT("1.5.94");DATWERT("19.9.94");4;3)Ergebnis: 19.03.1994Berechnet das Datum des letzten Zinstermins vor der Abrechnung.
Abrechnung ist der Kauftermin, Fälligkeit der Rücknahmetermin. Häufigkeit ist die Zahl der jährlichen Zinsausschüttungen (1, 2 oder 4). Basis gibt an, nach welchem Zeitsystem die Zinstage berechnet werden. Vgl. hierzu die Vorbemerkungen zu den Finanzfunktionen.
ZINSTERMZAHL()
Syntax: ZINSTERMZAHL(Abrechnung;Fälligkeit;Häufigkeit;Basis)Beispiel: ZINSTERMZAHL(DATWERT("1.5.94");DATWERT("19.9.94");4;3)Ergebnis: 2Berechnet die Zahl der Zinstermine zwischen dem Kaufdatum und dem Fälligkeitsdatum.
Abrechnung ist der Kauftermin, Fälligkeit der Rücknahmetermin. Häufigkeit ist die Zahl der jährlichen Zinsausschüttungen (1, 2 oder 4). Basis gibt an, nach welchem Zeitsystem die Zinstage berechnet werden. Vgl. hierzu die Vorbemerkungen zu den Finanzfunktionen.
ZINSZ()
Syntax: ZINSZ(Zins;Zr;Zzr;Bw;Zw;F)Beispiel: ZINSZ(8 %;5;12;8000)Ergebnis: -488,03 EURODie Funktion ermittelt den Zinsanteil für die Abzahlung eines Darlehens bei gleich bleibenden Zahlungen und bei gleich bleibendem Zinssatz (vgl. KAPZ und RMZ).
Argumente sind Zins, Zzr (die Zahlungszeiträume) und Bw (der Barwert, die Investition). Optional kann außer F (Fälligkeit; 0 für Ende der Perioden, 1 für Anfang) noch Zw (Zukunftswert) eingegeben werden. Vgl. KAPZ().
ZW()
Syntax: ZW(Zins;Zzr;Rmz;Bw;F)Beispiel: ZW(7 %;8;2400)Ergebnis: -24623,53 EURODie Funktion liefert als Ergebnis den zukünftigen Wert auf der Grundlage gleicher Zahlungen zu gleichem Zinssatz über die Laufzeit.
Mit Zins wird der Zins und mit Zzr werden die Zahlungszeiträume (oder die Anzahl der Zahlungen) angegeben.
Außer dem Betrag, der periodisch zu zahlen ist (Rmz oder auch die Ratenzahlung), können noch zwei optionale Argumente angegeben werden. Bw ist der gegenwärtige Barwert (bei Einzahlungen auf der Bank etwa der gegenwärtige Kontostand). Wird Bw nicht angegeben, so wird er als 0 angenommen.
Mit F wird angegeben, ob die Zahlungen jeweils am Ende einer Periode erfolgen (F = 0) oder am Anfang (F = 1).
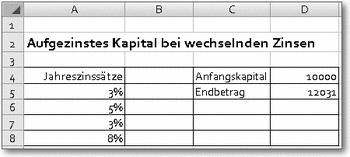
ZW2()
Syntax: ZW2(Kapital;Zinsen)Beispiel: siehe AbbildungBerechnet den Endwert eines Kapitals, das über mehrere Jahre mit jährlich wechselnden Zinsen verzinst wird.
Kapital ist das zum Anfang eingesetzte Kapital, Zinsen sind die jeweiligen Zinssätze. Implizit werden die Jahre mitgerechnet aus der Zahl der eingegebenen Zinssätze.
Verzinsung mit wechselnden Zinssätzen
ZZR()
Syntax: ZZR(Zins;Rmz;Bw;Zw;F)Beispiel: ZZR(5 %;-1000;10000)Ergebnis: 14,2Die Funktion berechnet die Zahl der Zahlungsperioden, z. B. zur Tilgung eines Darlehens, wenn die Zahlungen zu einem gleich bleibendem Zinssatz erfolgen.
Mit Zins und Rmz wird der Zinssatz und der Betrag der jeweiligen Zahlung angegeben. Bw ist der Betrag, der durch die Zahlungen erreicht werden soll (z. B. die Höhe des Darlehens). Die optionalen Argumente Zw und F stehen für den Zukunftswert (welcher Betrag soll am Ende vorhanden sein) und die Fälligkeit der Zahlungen (F = 0 für Ende der Perioden). Werden diese Argumente nicht angegeben, dann werden sie mit 0 angenommen.
Ihre Meinung
Wie hat Ihnen das Openbook gefallen? Wir freuen uns immer über Ihre Rückmeldung. Schreiben Sie uns gerne Ihr Feedback als E-Mail an kommunikation@rheinwerk-verlag.de.




 Jetzt bestellen
Jetzt bestellen



