9.4 Mehrfachverteilung und Zyklen – Ring– und Netzdiagramme 

Besondere Anforderungen sind an ein Diagramm gestellt, wenn es darum geht, nicht nur in einem einzigen Fall die Verteilung von Werten zu einem Ganzen darzustellen, sondern gleich in mehreren. Ähnliches gilt für die Darstellung von Werten, die sich in einer bestimmten Abfolge ändern.

Ringdiagramm zum Vergleich von Datengruppen 

Das Ringdiagramm bildet quasi eine Kombination mehrerer Kreisdiagramme, die aber nicht nebeneinander, sondern ineinander angeordnet sind. Bei mehreren Datengruppen, die anteilsmäßig dargestellt werden sollen, gibt es in Excel einige Alternativen. Sie lassen sich als gestaffelte Säulen, Balken oder als gestapelte Flächen abbilden. Die Darstellung in mehreren Kreisdiagrammen ist ebenfalls ein gangbarer Weg, besonders wenn zwischen den verschiedenen Datenreihen keine Hierarchie beabsichtigt ist.

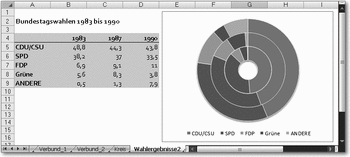
Das folgende Beispiel zeigt die Wahlergebnisse für drei Bundestagswahlen in einem. Das jüngste Ergebnis wird mit dem äußersten Ring dargestellt.

Sofern es sich nicht um allzu viele Datengruppen handelt, bietet sich das Ringdiagramm an, das aber durchaus eine Hierarchie setzt. Bei der konzentrischen Anordnung der Kreise sollte zumindest darauf geachtet werden, dass etwaige zeitliche Abfolgen so aufgenommen werden, dass die »früheren« Datengruppen innen sitzen, die »späteren« oder die »wichtigeren« außen. Als Legende verfügt dieser Diagrammtyp über die Angaben für die einzelnen Ringsegmente.

Ringdiagramm als Kombination mehrerer Kreisdiagramme

Bei den Ringdiagrammen werden nur zwei Untertypen angeboten, ohne oder mit Ausrückung der Ringsegmente. Bei den Ausrückungen ist hier, wie auch schon bei den Kreisdiagrammen, zu empfehlen, diese direkt im Diagramm mit der Maus vorzunehmen.

Häufig ist es sinnvoll, über Datenreihen formatieren auf dem Register Reihenoptionen die Innenringgröße zu verringern (der Minimalwert ist 10  %, der Maximalwert 90  %). Dadurch bleibt mehr Raum für die Darstellung der Daten. Außerdem können Sie hier durch eine Veränderung des Winkels für das erste Segment den Ring in eine beliebige Position drehen.

Netzdiagramme für Zyklen

Das Netzdiagramm ähnelt noch am ehesten einem Polarkoordinaten-Diagramm, allerdings mit drei Unterscheidungen:

• Der Winkel ist nicht direkt angebbar, sondern wird durch die Anzahl der Werte bestimmt.

• Die Richtung bzw. Reihenfolge geht mit dem Uhrzeigersinn (bei Polarkoordinaten gegen den Uhrzeigersinn).

• Die Größenachsen dürfen auch negative Werte annehmen.

Anwendbar ist das Netzdiagramm für die Abbildung aller zyklischen Prozesse oder Daten. Das kann die Helligkeit in Abhängigkeit vom Winkel sein, die Temperatur oder die Niederschlagsmenge im Laufe eines Tages oder Jahres, die Wachstumsrate einer Pflanze in einem Jahreszyklus usw. Im Prinzip ist es auch bei diesem Diagrammtyp möglich, mehrere Datenreihen zu verarbeiten, aber bei mehr als zwei oder drei Datenreihen wird das Diagramm ziemlich unübersichtlich.

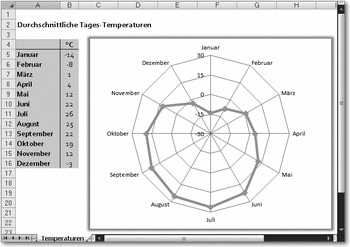
Das (fiktive) Beispiel zeigt die durchschnittliche tägliche Temperatur in einem Land über die zwölf Monate eines Jahres:

Netzdiagramm für die Darstellung von Temperaturzyklen

Die Untertypen des Netzdiagramms 

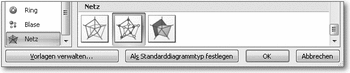
An Untertypen bietet das Netzdiagramm eine Version ohne Datenpunkte, einen Untertyp mit Datenpunkten, wie in der Beispielabbildung, und einen Untertyp, bei dem die Datenlinie flächig ausgefüllt ist.

Untertypen der Netzdiagramme

Bei der Bearbeitung eines Netzdiagramms kommen vor allem zwei Punkte in Frage. Zum einen sollten die Datenlinie und die Datenpunkte so gewählt werden, dass sie in der Darstellung gut sichtbar sind, zum anderen bieten sich für die Formatierung der Achsen alle üblichen Möglichkeiten:

• Durch geschickte Skalierung kann dafür gesorgt werden, dass tatsächlich alle Werte gut ablesbar sind.

• Durch geeignete Wahl der Intervalle lässt sich gewährleisten, dass die Achsenbeschriftung nicht mit den Daten kollidiert.

Ihre Meinung

Wie hat Ihnen das Openbook gefallen? Wir freuen uns immer über Ihre Rückmeldung. Schreiben Sie uns gerne Ihr Feedback als E-Mail an kommunikation@rheinwerk-verlag.de.