12.4 Ganzzahlen – int 

Für den Raum der ganzen Zahlen gibt es in Python den Datentypen int. Im Gegensatz zu vielen anderen Programmiersprachen unterliegt dieser Datentyp in seinem Wertebereich keinen prinzipiellen Grenzen, was den Umgang mit großen ganzen Zahlen in Python sehr komfortabel macht.[ 29 ](Dies ist eine Neuerung in Python 3.0. Zuvor existierten zwei Datentypen für ganze Zahlen: int für den begrenzten Zahlenraum von 32 Bit bzw. 64 Bit sowie long mit einem unbegrenzten Wertebereich.)
Wir haben bereits viel mit ganzen Zahlen gearbeitet, sodass die Verwendung von int eigentlich keiner Demonstration mehr bedarf. Der Vollständigkeit halber dennoch ein kleines Beispiel:
>>> i = 1234
>>> i
1234
>>> p = int(5678)
>>> p
5678
Seit Python 3.6 kann ein Unterstrich verwendet werden, um die Ziffern eines Literals zu gruppieren:
>>> 1_000_000
1000000
>>> 1_0_0
100
Die Gruppierung ändert nichts am Zahlenwert des Literals, sondern dient dazu, die Lesbarkeit von Zahlenliteralen zu erhöhen. Ob und wie Sie die Ziffern gruppieren, bleibt Ihnen überlassen.
12.4.1 Zahlensysteme 

Ganze Zahlen können in Python in mehreren Zahlensystemen[ 30 ](Sollten Sie nicht wissen, was ein Zahlensystem ist, können Sie diesen Abschnitt problemlos überspringen. ) geschrieben werden:
-
Zahlen, die wie im oben dargestellten Beispiel ohne ein spezielles Präfix geschrieben sind, werden im Dezimalsystem (Basis 10) interpretiert. Beachten Sie, dass einer solchen Zahl keine führenden Nullen vorangestellt werden dürfen:
v_dez = 1337 -
Das Präfix 0o (»Null-o«) kennzeichnet eine Zahl, die im Oktalsystem (Basis 8) geschrieben wurde. Beachten Sie, dass hier nur Ziffern von 0 bis 7 erlaubt sind:
Das kleine »o« im Präfix kann auch durch ein großes »O« ersetzt werden. Wir empfehlen Ihnen jedoch, stets ein kleines »o« zu verwenden, da das große »O« in vielen Schriftarten von der Null kaum zu unterscheiden ist.[ 31 ](Bis zu Version 3.0 wurde in Python, wie beispielsweise in C auch, die »0« als Präfix für Oktalzahlen verwendet. )
v_okt = 0o2471 -
Die nächste und weitaus gebräuchlichere Variante ist das Hexadezimalsystem (Basis 16), das durch das Präfix 0x bzw. 0X (Null-x) gekennzeichnet wird. Die Zahl selbst darf aus den Ziffern 0–9 und den Buchstaben A–F bzw. a–f gebildet werden:
v_hex = 0x5A3F -
Neben dem Hexadezimalsystem ist in der Informatik das Dualsystem, auch Binärsystem (Basis 2), von entscheidender Bedeutung. Seit Version 3.0 unterstützt Python ein eigenes Literal für Dualzahlen. Diese werden analog zu den vorangegangenen Literalen durch das Präfix 0b eingeleitet:
Im Dualsystem dürfen nur die Ziffern 0 und 1 verwendet werden.
v_bin = 0b1101
Vielleicht möchten Sie sich nicht auf diese vier Zahlensysteme beschränken, die von Python explizit unterstützt werden, sondern ein exotischeres verwenden. Natürlich gibt es in Python nicht für jedes mögliche Zahlensystem ein eigenes Literal. Stattdessen können Sie sich folgender Schreibweise bedienen:
v_6 = int("54425", 6)
Es handelt sich um eine alternative Methode, eine Instanz des Datentyps int zu erzeugen und mit einem Anfangswert zu versehen. Dazu werden in den Klammern ein String, der den gewünschten Initialwert in dem gewählten Zahlensystem enthält, sowie die Basis dieses Zahlensystems als ganze Zahl geschrieben. Beide Werte müssen durch ein Komma getrennt werden. Im Beispiel wurde das Sechsersystem verwendet.
Python unterstützt Zahlensysteme mit einer Basis von 2 bis 36. Wenn ein Zahlensystem mehr als zehn verschiedene Ziffern zur Darstellung einer Zahl benötigt, werden zusätzlich zu den Ziffern 0 bis 9 die Buchstaben A bis Z des englischen Alphabets verwendet.
v_6 hat jetzt den Wert 7505 im Dezimalsystem.
Für alle Zahlensystem-Literale ist die Verwendung eines negativen Vorzeichens möglich:
>>> -1234
-1234
>>> -0o777
-511
>>> -0xFF
-255
>>> -0b1010101
-85
Beachten Sie, dass es sich bei den Zahlensystemen nur um eine alternative Schreibweise des gleichen Wertes handelt. Der Datentyp int springt beispielsweise nicht in eine Art Hexadezimalmodus, sobald er einen solchen Wert enthält, sondern das Zahlensystem ist nur bei Zuweisungen oder Ausgaben von Bedeutung. Standardmäßig werden alle Zahlen im Dezimalsystem ausgegeben:
>>> v1 = 0xFF
>>> v2 = 0o777
>>> v1
255
>>> v2
511
Wir werden später im Zusammenhang mit Strings darauf zurückkommen, wie sich Zahlen in anderen Zahlensystemen ausgeben lassen.
12.4.2 Bit-Operationen 

Wie bereits gesagt, hat das Dualsystem oder auch Binärsystem in der Informatik eine große Bedeutung. Für den Datentyp int sind daher einige zusätzliche Operatoren definiert, die sich explizit auf die binäre Darstellung der Zahl beziehen:
| Operator | Erw. Zuweisung | Ergebnis |
|---|---|---|
| x & y | x &= y | bitweises UND von x und y (AND) |
| x | y | x |= y | bitweises nicht ausschließendes ODER von x und y (OR) |
| x ^ y | x ^= y | bitweises ausschließendes ODER von x und y (XOR) |
| ~x | bitweises Komplement von x | |
| x << n | x <<= n | Bit-Verschiebung um n Stellen nach links |
| x >> n | x >>= n | Bit-Verschiebung um n Stellen nach rechts |
Tabelle 12.5 Bit-Operatoren des Datentyps int
Da vielleicht nicht jedem unmittelbar klar ist, was die einzelnen Operationen bewirken, möchten wir sie im Folgenden im Detail besprechen.
Bitweises UND
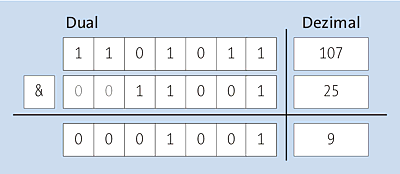
Das bitweise UND zweier Zahlen wird gebildet, indem beide Zahlen in ihrer Binärdarstellung Bit für Bit miteinander verknüpft werden. Die resultierende Zahl hat in ihrer Binärdarstellung genau dort eine 1, wo beide der jeweiligen Bits der Operanden 1 sind, und sonst eine 0. Dies veranschaulicht Abbildung 12.1:
Abbildung 12.1 Bitweises UND
Im interaktiven Modus von Python probieren wir aus, ob das bitweise UND mit den in der Grafik gewählten Operanden tatsächlich das erwartete Ergebnis zurückgibt:
>>> 107 & 25
9
Diese Prüfung des Ergebnisses werden wir nicht für jede Operation einzeln durchführen. Um allerdings mit den bitweisen Operatoren vertrauter zu werden, lohnt es sich, hier ein wenig zu experimentieren.
Bitweises ODER
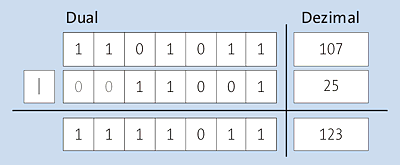
Das bitweise ODER zweier Zahlen wird gebildet, indem beide Zahlen in ihrer Binärdarstellung Bit für Bit miteinander verglichen werden. Die resultierende Zahl hat in ihrer Binärdarstellung genau da eine 1, wo mindestens eines der jeweiligen Bits der Operanden 1 ist. Abbildung 12.2 veranschaulicht dies.
Abbildung 12.2 Bitweises nicht ausschließendes ODER
Bitweises ausschließendes ODER
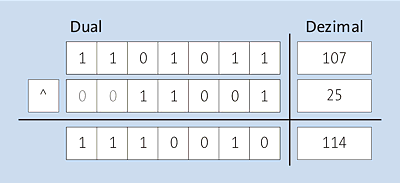
Das bitweise ausschließende ODER (auch exklusives ODER) zweier Zahlen wird gebildet, indem beide Zahlen in ihrer Binärdarstellung Bit für Bit miteinander verglichen werden. Die resultierende Zahl hat in ihrer Binärdarstellung genau da eine 1, wo sich die jeweiligen Bits der Operanden voneinander unterscheiden, und eine 0, wo sie gleich sind. Dies zeigt Abbildung 12.3.
Abbildung 12.3 Bitweises exklusives ODER
Bitweises Komplement
Das bitweise Komplement bildet das sogenannte Einerkomplement einer Dualzahl, das der Negation aller vorkommenden Bits entspricht. In Python ist dies auf Bit-Ebene nicht möglich, da eine ganze Zahl in ihrer Länge unbegrenzt ist und das Komplement immer in einem abgeschlossenen Zahlenraum gebildet werden muss. Deswegen wird die eigentliche Bit-Operation zur arithmetischen Operation und ist folgendermaßen definiert:[ 32 ](Das ist sinnvoll, da man zur Darstellung negativer Zahlen in abgeschlossenen Zahlenräumen
das sogenannte Zweierkomplement verwendet. Dieses erhalten Sie, indem Sie zum Einerkomplement 1 addieren.
Also: –x = Zweierkomplement von x = ~x + 1
Daraus folgt: ~x = –x – 1
)
~x = –x–1
Bit-Verschiebung
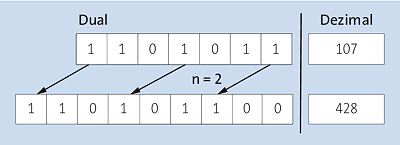
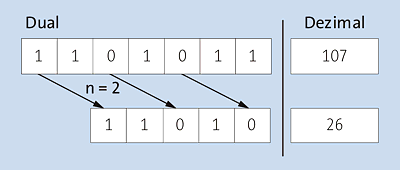
Bei der Bit-Verschiebung wird die Bit-Folge in der binären Darstellung des ersten Operanden um die durch den zweiten Operanden gegebene Anzahl Stellen nach links bzw. rechts verschoben. Auf der rechten Seite entstehende Lücken werden mit Nullen gefüllt, und das Vorzeichen des ersten Operanden bleibt erhalten. Abbildung 12.4 und Abbildung 12.5 veranschaulichen eine Verschiebung um zwei Stellen nach links bzw. nach rechts.
Abbildung 12.4 Bit-Verschiebung um zwei Stellen nach links
Abbildung 12.5 Bit-Verschiebung um zwei Stellen nach rechts
Die in der Bit-Darstellung entstehenden Lücken auf der rechten bzw. linken Seite werden mit Nullen aufgefüllt.
Die Bit-Verschiebung ist in Python ähnlich wie der Komplementoperator arithmetisch implementiert. Ein Shift um x Stellen nach rechts entspricht einer ganzzahligen Division durch 2x. Ein Shift um x Stellen nach links entspricht einer Multiplikation mit 2x.
12.4.3 Methoden 

Der Datentyp int verfügt über eine Methode, die sich auf die Binärdarstellung der ganzen Zahl bezieht. Die Methode bit_length berechnet die Anzahl Stellen, die für die Binärdarstellung der Zahl benötigt werden.
>>> (36).bit_length()
6
>>> (4345).bit_length()
13
Die Binärdarstellung der 36 ist 100100, und die der 4345 ist 1000011111001. Damit benötigen die beiden Zahlen 6 bzw. 13 Stellen für ihre Binärdarstellung.
[»] Hinweis
Beachten Sie, dass die Klammern um die Zahlenliterale bei ganzen Zahlen benötigt werden, da es sonst zu Doppeldeutigkeiten mit der Syntax für Gleitkommazahlen kommen könnte.


 Python 3
Python 3 Jetzt Buch bestellen
Jetzt Buch bestellen





