26 Mathematik 

Wir beginnen mit den Modulen der Standardbibliothek, mit deren Hilfe sich im weitesten Sinne mathematische Berechnungen durchführen lassen. Tabelle 26.1 listet die Module auf, die in diesem Kapitel besprochen werden.
| Modul | Beschreibung | Abschnitt |
|---|---|---|
| math | mathematische Funktionen | 26.1 |
| cmath | mathematische Funktionen für komplexe Zahlen | 26.1 |
| random | Erzeugen von Zufallszahlen oder zufälligen Auswahlen aus gegebenen Mengen | 26.2 |
| decimal | präzise Repräsentation von Dezimalzahlen | 26.3 |
Tabelle 26.1 Mathematische Module der Standardbibliothek
26.1 Mathematische Funktionen – math, cmath 

Das Modul math ist Teil der Standardbibliothek und stellt mathematische Funktionen und Konstanten bereit.
[»] Hinweis
Das Modul math berücksichtigt den komplexen Zahlenraum – und damit den Datentyp complex – nicht. Das heißt vor allem, dass eine in math enthaltene Funktion niemals einen komplexen Parameter akzeptiert oder ein komplexes Ergebnis zurückgibt.
Sollte ein komplexes Ergebnis ausdrücklich gewünscht sein, kann anstelle von math das Modul cmath verwendet werden, in dem die Funktionen von math enthalten sind, die eine sinnvolle Erweiterung auf den komplexen Zahlen haben.
In den folgenden Abschnitten werden die in math bzw. cmath enthaltenen Funktionen thematisch gruppiert vorgestellt. In den jeweiligen Tabellen wird in der Spalte cmath angegeben, ob eine Funktion auch im Modul cmath enthalten ist.
Abgesehen von einer Fülle von Funktionen definieren die Module math und cmath sechs Konstanten:
| Konstante | Beschreibung | cmath |
|---|---|---|
| e | die Eulersche Zahl e | ja |
| pi | die Kreiszahl Pi (π) | ja |
| inf | der Wert »unendlich«, äquivalent zu float("inf") | ja |
| nan | der Wert »Not a Number«, äquivalent zu float("nan") | ja |
| infj | der komplexe Wert »unendlich«, äquivalent zu float("infj") | nur |
| nanj | der komplexe Wert »Not a Number«, äquivalent zu float("nanj") | nur |
Tabelle 26.2 Konstanten der Module math und cmath
Bevor Sie die folgenden Beispiele im interaktiven Modus verwenden können, müssen Sie math oder cmath einbinden:
>>> import math
>>> import cmath
26.1.1 Zahlentheoretische Funktionen 

Die Module math bzw. cmath definieren die zahlentheoretischen Funktionen in Tabelle 26.3.
| Funktion | Beschreibung | cmath |
|---|---|---|
| ceil(x) | Rundet auf die nächsthöhere Ganzzahl auf. | nein |
| copysign(x, y) | Überträgt das Vorzeichen von y auf x und gibt das Ergebnis zurück. | nein |
| fabs(x) | Gibt den Betrag von x zurück. Das Ergebnis ist immer eine Gleitkommazahl. | nein |
| factorial(x) | Berechnet die Fakultät der ganzen Zahl x. | nein |
| floor(x) | Rundet auf die nächstniedrigere Ganzzahl ab. | nein |
| fmod(x, y) | Berechnet x Modulo y. | nein |
| frexp(x) | Extrahiert Mantisse und Exponent von x. | nein |
| fsum(iterable) | Berechnet die Summe der in iterable enthaltenen Gleitkommazahlen. | nein |
| gcd(x, y) | Gibt den größten gemeinsamen Teiler von x und y zurück. | nein |
| isclose(a, b, {rel_tol, abs_tol}) | Gibt genau dann True zurück, wenn a und b hinreichend nah beieinander liegen. Die zulässigen Toleranzen können über rel_tol und abs_tol relativ und/oder absolut festgelegt werden. | ja |
| isfinite(x) | Gibt genau dann True zurück, wenn x keinen der Werte inf, -inf oder nan referenziert.* | ja |
| isinf(x) | Gibt genau dann True zurück, wenn x positiv oder negativ unendlich ist. | ja |
| isnan(x) | Gibt genau dann True zurück, wenn x den Wert nan hat. | ja |
| ldexp(m, e) | Bestimmt eine Gleitkommazahl aus Mantisse m und Exponent e. | nein |
| modf(x) | Gibt ein Tupel mit dem Nachkomma- und dem Vorkommaanteil der Gleitkommazahl x zurück. | nein |
| trunc(x) | Gibt den Vorkommaanteil von x als ganze Zahl zurück. Verhält sich bei positiven Werten von x wie floor und bei negativen Werten von x wie ceil. | nein |
| * Diese Werte stehen für positiv und negativ unendlich bzw. »Not a Number«. Näheres dazu erfahren Sie in Abschnitt 26.3.2, »Nichtnumerische Werte«. | ||
Tabelle 26.3 Zahlentheoretische Funktionen in math und cmath
Im Folgenden finden Sie detaillierte Erklärungen zu einer Auswahl der oben vorgestellten Funktionen.
fmod(x, y)
Die Funktion fmod berechnet x Modulo y. Beachten Sie, dass diese Funktion nicht immer dasselbe Ergebnis berechnet wie x % y. So gibt fmod das Ergebnis mit dem Vorzeichen von x zurück, während x % y das Ergebnis mit dem Vorzeichen von y zurückgibt. Generell gilt, dass fmod bei Modulo-Operationen mit Gleitkommazahlen bevorzugt werden sollte und der Modulo-Operator % bei Operationen mit ganzen Zahlen.
>>> math.fmod(7.5, 3.5)
0.5
frexp(x)
Die Funktion frexp extrahiert Mantisse und Exponent der übergebenen Zahl x. Das Ergebnis ist ein Tupel der Form (m, e), wobei m für die Mantisse und e für den Exponenten steht. Mantisse und Exponent sind dabei im Kontext der Formel x = m ⋅ 2e zu verstehen.
>>> math.frexp(2.5)
(0.625, 2)
fsum(iterable)
Die Funktion fsum berechnet die Summe der in iterable enthaltenen Gleitkommazahlen.
>>> math.fsum([1.5, 7.34, 2, 4.78])
15.620000000000001
Der Vorteil von fsum gegenüber der Built-in Function sum, die prinzipiell für den gleichen Zweck eingesetzt werden kann, ist, dass fsum versucht, die durch die Summation in der Gleitkommaarithmetik entstehenden Fehler möglichst gering zu halten. Das Ergebnis von fsum ist also genauer als das Ergebnis von sum.
26.1.2 Exponential- und Logarithmusfunktionen 

Die Module math bzw. cmath definieren die folgenden Funktionen, die sich auf die Exponential- bzw. Logarithmusfunktion beziehen:
| Funktion | Beschreibung | cmath |
|---|---|---|
| exp(x) | Berechnet ex. | ja |
| log(x, [base]) | Berechnet den Logarithmus von x zur Basis base. Wenn base nicht angegeben wurde, wird der Logarithmus Naturalis (Basis e) berechnet. | ja |
| log10(x) | Berechnet den Logarithmus von x zur Basis 10. | ja |
| log2(x) | Berechnet den Logarithmus von x zur Basis 2. | nein |
| pow(x, y) | Berechnet xy. | nein |
| sqrt(x) | Berechnet die Quadratwurzel von x. | ja |
Tabelle 26.4 Exponential- und Logarithmusfunktionen in math und cmath
26.1.3 Trigonometrische und hyperbolische Funktionen 

Die Module math bzw. cmath definieren die folgenden trigonometrischen Funktionen:
Tabelle 26.5 Trigonometrische und hyperbolische Funktionen der Module math und cmath
26.1.4 Umrechnen von Winkeln 

Zum Umrechnen von Winkeln zwischen Radiant und Grad enthält das Modul math die Funktionen degrees und radians:
>>> math.degrees(math.pi/2)
90.0
>>> math.radians(90)
1.5707963267948966
26.1.5 Darstellungsformen komplexer Zahlen 

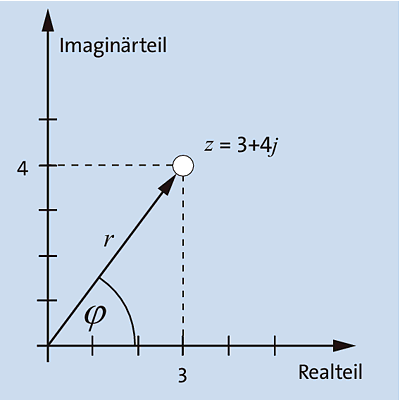
Die in cmath enthaltenen Funktionen phase, polar und rect eignen sich dazu, verschiedene Darstellungsformen komplexer Zahlen ineinander umzurechnen. Dazu wird eine komplexe Zahl a + bj als Punkt (a,b) im zweidimensionalen Raum aufgefasst. Dieser Raum wird die gaußsche Zahlenebene genannt. Die komplexe Zahl lässt sich jetzt entweder in kartesischen Koordinaten über die Werte a und b ausdrücken oder in Polarkoordinaten mithilfe des Winkels φ und des Radius r. Abbildung 26.1 zeigt die beiden Darstellungsformen komplexer Zahlen an einem Beispiel.
Abbildung 26.1 Die zwei Darstellungen der komplexen Zahl 3+4j
Die Funktionen phase, polar und rect erlauben es, eine komplexe Zahl in kartesischen Koordinaten oder in Polarkoordinaten darzustellen:
>>> cmath.phase(3+4j)
0.9272952180016122
>>> cmath.polar(3+4j)
(5.0, 0.9272952180016122)
>>> cmath.rect(5.0, 0.9272952180016122)
(3.0000000000000004+3.9999999999999996j)


 Python 3
Python 3 Jetzt Buch bestellen
Jetzt Buch bestellen





