26.3 Präzise Dezimalzahlen – decimal 

Sicherlich erinnern Sie sich noch an folgendes Beispiel, das zeigt, dass bei der Verwendung des eingebauten Datentyps float Rechenfehler auftreten:
>>> 1.1 + 2.2
3.3000000000000003
Das liegt daran, dass nicht jede Dezimalzahl durch das interne Speichermodell von float dargestellt werden kann, sondern nur mit einer gewissen Genauigkeit angenähert wird.[ 110 ](Dabei handelt es sich nicht um ein Python-spezifisches Problem, sondern um eine grundsätzliche Einschränkung der Gleitkommadarstellung im Computer. ) Diese Rechenfehler werden jedoch in der Regel aus Gründen der Effizienz in Kauf genommen. In einigen Fällen, beispielsweise beim Rechnen mit Geldbeträgen, ist die Exaktheit des Ergebnisses jedoch wichtiger als die Rechenzeit. Als wir über Gleitkommazahlen gesprochen haben, haben wir Ihnen Abhilfe durch ein Modul versprochen, und dieses Modul heißt decimal. Wir müssen aber deutlich darauf hinweisen, dass diese Abhilfe auf Kosten der Performance geht.
Das Modul decimal enthält den Datentyp Decimal, der Dezimalzahlen mit einer beliebigen Präzision speichern und verarbeiten kann:
>>> from decimal import Decimal
[»] Hinweis
Das hier besprochene Modul decimal folgt in seiner Funktionsweise der General Decimal Arithmetic Specification von IBM. Aus diesem Grund ist es möglich, dass Ihnen ein ähnliches Modul bereits von einer anderen Programmiersprache her bekannt ist.
Es existieren beispielsweise Bibliotheken, die das decimal-Modul in gleicher oder abgewandelter Form für C, C++, Java oder Perl implementieren.
26.3.1 Verwendung des Datentyps 

Es gibt kein Literal, mit dem Sie Instanzen des Datentyps Decimal direkt erzeugen könnten, wie es beispielsweise bei float der Fall ist. Um eine Decimal-Instanz mit einem bestimmten Wert zu erzeugen, müssen Sie den Datentyp explizit instanziieren. Den Wert können Sie dem Konstruktor in Form eines Strings übergeben:
>>> Decimal("0.9")
Decimal('0.9')
>>> Decimal("1.33e7")
Decimal('1.33E+7')
Dies ist die geläufigste Art, Decimal zu instanziieren. Es ist außerdem möglich, dem Konstruktor eine ganze Zahl oder ein Tupel zu übergeben:
>>> Decimal(123)
Decimal('123')
>>> Decimal((0, (3, 1, 4, 1), -3))
Decimal('3.141')
Im Fall eines Tupels bestimmt das erste Element das Vorzeichen, wobei 0 für eine positive und 1 für eine negative Zahl steht. Das zweite Element muss ein weiteres Tupel sein, das alle Ziffern der Zahl enthält. Das dritte Element des Tupels ist die Verschiebung des Dezimalpunktes in der im vorangegangenen Element angegebenen Zahl.
[»] Hinweis
Seit Python 3.2 ist es möglich, dem Konstruktor der Decimal-Klasse eine Gleitkommazahl direkt zu übergeben:
>>> Decimal(0.7)
Decimal('0.6999999999999999555910790149937383830547332763671875')
Dabei sollten Sie stets im Hinterkopf behalten, dass sich dann die Ungenauigkeit von float bei der Initialisierung auf die Decimal-Instanz überträgt.
Sobald eine Decimal-Instanz erzeugt wurde, kann sie wie eine Instanz eines numerischen Datentyps verwendet werden. Das bedeutet insbesondere, dass alle von diesen Datentypen her bekannten Operatoren auch für Decimal definiert sind. Es ist zudem möglich, Decimal in Operationen mit anderen numerischen Datentypen zu verwenden. Kurzum: Decimal fügt sich gut in die bestehende Welt der numerischen Datentypen ein.
>>> Decimal("0.9") * 5
Decimal('4.5')
>>> Decimal("0.9") / 10
Decimal('0.09')
>>> Decimal("0.9") % Decimal("1.0")
Decimal('0.9')
Eine Besonderheit des Datentyps ist es, abschließende Nullen beim Nachkommaanteil einer Dezimalzahl beizubehalten, obwohl diese eigentlich überflüssig sind. Das ist beispielsweise beim Rechnen mit Geldbeträgen von Nutzen:
>>> Decimal("2.50") + Decimal("4.20")
Decimal('6.70')
Decimal-Instanzen können untereinander oder mit Instanzen anderer numerischer Datentypen verglichen werden.
>>> Decimal("0.7") < Decimal("0.8")
True
>>> Decimal(0.7) == 0.7
True
>>> Decimal("0.7") == 0.7
False
Ein Decimal-Wert lässt sich in einen Wert eines beliebigen anderen numerischen Datentyps überführen. Beachten Sie, dass diese Konvertierungen in der Regel verlustbehaftet sind, der Wert also an Genauigkeit verliert.
>>> float(Decimal("1.337"))
1.337
>>> float(Decimal("0.9"))
0.9
>>> int(Decimal("1.337"))
1
Diese Eigenschaft ermöglicht es, Decimal-Instanzen ganz selbstverständlich als Parameter etwa von Built-in Functions oder Funktionen der Bibliothek math zu übergeben:
>>> import math
>>> math.sqrt(Decimal("2"))
1.4142135623730951
[»] Hinweis
Auch wenn Decimal-Instanzen an Funktionen des Moduls math übergeben werden können, geben diese Funktionen niemals eine Decimal-Instanz zurück. Sie laufen also Gefahr, durch den float-Rückgabewert an Genauigkeit zu verlieren.
Für einige mathematische Funktionen stellt eine Decimal-Instanz spezielle Methoden bereit. Jede dieser Methoden erlaubt es, neben ihren spezifischen Parametern ein sogenanntes Context-Objekt zu übergeben. Ein solches Context-Objekt beschreibt den Kontext, in dem die Berechnungen durchgeführt werden sollen, beispielsweise auf wie viele Nachkommastellen genau gerundet werden soll. Näheres zum Context-Objekt erfahren Sie weiter hinten in diesem Abschnitt.
Die wichtigsten Methoden einer Decimal-Instanz d sind:
| Methode | Bedeutung |
|---|---|
| d.exp([context]) | ed |
| d.fma(other, third[, context]) | d⋅other+third* |
| d.ln([context]) | loge(d) |
| d.log10([context]) | log10(d) |
| d.logb([context]) | logb(d) |
| d.sqrt([context]) | 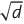 |
| d.as_integer_ratio() | Gibt Zähler und Nenner von d als Tupel zurück. |
| * Der Vorteil dieser Methode ist, dass sie die Berechnung »in einem Guss« durchführt, dass also nicht mit einem gerundeten Zwischenergebnis der Multiplikation weitergerechnet wird. | |
Tabelle 26.6 Mathematische Methoden des Datentyps Decimal
Die Verwendung dieser Methoden demonstriert das folgende Beispiel:
>>> d = Decimal("9")
>>> d.sqrt()
Decimal('3')
>>> d.ln()
Decimal('2.197224577336219382790490474')
>>> d.fma(2, -7)
Decimal('11')
[»] Hinweis
Das Programmieren mit dem Datentyp Decimal ist mit viel Schreibarbeit verbunden, da kein Literal für diesen Datentyp existiert. Viele Python-Programmierer behelfen sich damit, dem Datentyp einen kürzeren Namen zu verpassen:
>>> from decimal import Decimal as D
>>> D("1.5e-7")
Decimal('1.5E-7')
26.3.2 Nichtnumerische Werte 

Aus Abschnitt 12.5, »Gleitkommazahlen – float«, kennen Sie bereits die Werte nan und inf des Datentyps float, die immer dann auftreten, wenn eine Berechnung nicht möglich ist bzw. eine Zahl den Zahlenraum von float sprengt. Der Datentyp Decimal baut auf diesem Ansatz auf und ermöglicht es Ihnen, Decimal-Instanzen mit einem solchen Zustand zu initialisieren. Folgende Werte sind möglich:
| Wert | Bedeutung |
|---|---|
| Infinity, Inf | positiv unendlich |
| -Infinity, -Inf | negativ unendlich |
| NaN | ungültiger Wert (»Not a Number«) |
| sNaN | ungültiger Wert (»signaling Not a Number«)* |
| * Der Unterschied zu NaN besteht darin, dass eine Exception geworfen wird, sobald versucht wird, mit sNaN weiterzurechnen. Rechenoperationen mit NaN werden durchgeführt, ergeben allerdings immer wieder NaN. | |
Tabelle 26.7 Nichtnumerische Werte des Datentyps Decimal
Diese nichtnumerischen Werte können wie Zahlen verwendet werden:
>>> Decimal("NaN") + Decimal("42.42")
Decimal('NaN')
>>> Decimal("Infinity") + Decimal("Infinity")
Decimal('Infinity')
>>> Decimal("sNaN") + Decimal("42.42")
Traceback (most recent call last):
File "<stdin>", line 1, in <module>
InvalidOperation: sNaN
>>> Decimal("Inf") - Decimal("Inf")
Traceback (most recent call last):
File "<stdin>", line 1, in <module>
InvalidOperation: -INF + INF
26.3.3 Das Context-Objekt 

Der Datentyp Decimal erlaubt es, Dezimalzahlen mit beliebiger Genauigkeit zu speichern. Die Genauigkeit, also die Anzahl der Nachkommastellen, ist eine von mehreren globalen Einstellungen, die innerhalb eines sogenannten Context-Objekts gekapselt werden.
Um auf den aktuellen Kontext der arithmetischen Operationen zugreifen zu können, existieren innerhalb des Moduls decimal die Funktionen getcontext und setcontext.
An dieser Stelle möchten wir nur auf drei Attribute des Context-Objekts eingehen, die die Berechnungen beeinflussen können.
prec
Das Attribut prec (für precision) bestimmt die Genauigkeit der Decimal-Instanzen des aktuellen Kontextes. Der Wert versteht sich als Anzahl der zu berechnenden Nachkommastellen und ist mit 28 vorbelegt.
>>> import decimal
>>> c = decimal.getcontext()
>>> c.prec = 3
>>> Decimal("1.23456789") * Decimal("2.3456789")
Decimal('2.90')
Emin, Emax
Die Attribute Emin und Emax legen die maximale bzw. minimale Größe des Exponenten fest. Beide müssen eine ganze Zahl referenzieren. Wenn das Ergebnis einer Berechnung dieses Limit überschreitet, wird eine Exception geworfen.
>>> import decimal
>>> c = decimal.getcontext()
>>> c.Emax = 9
>>> Decimal("1e100") * Decimal("1e100")
Traceback (most recent call last):
File "<stdin>", line 1, in <module>
Overflow: above Emax
Dieser Abschnitt versteht sich als grundlegende Einführung in das Modul decimal. Dieses Modul bietet noch viele weitere Möglichkeiten, Berechnungen anzustellen oder Ergebnisse dieser Berechnungen an die eigenen Bedürfnisse anzupassen. Sollte Ihr Interesse an diesem Modul geweckt worden sein, fühlen Sie sich dazu ermutigt, insbesondere in der Python-Dokumentation nach weiteren Verwendungswegen zu forschen.
Beachten Sie aber, dass üblicherweise kein Bedarf an solch präzisen Berechnungen besteht, wie sie der Datentyp Decimal ermöglicht. Der Geschwindigkeitsvorteil von float wiegt in der Regel schwerer als der Genauigkeitsgewinn von Decimal.


 Python 3
Python 3 Jetzt Buch bestellen
Jetzt Buch bestellen





