6.4 Normalisierung und Denormalisierung 

Normalisierung: Redundanz minimieren

Wir haben gerade einige Richtlinien vorgestellt, nach denen wir vorgehen sollten, wenn wir objektorientierte Klassenstrukturen auf Tabellen abbilden. Doch die relationalen Datenbanken sind unabhängig von der Objektorientierung. Die relationalen Datenbanken sind dabei einer der wenigen Bereiche der Softwareentwicklung, denen eine mathematisch begründete Theorie zugrunde liegt. Sie haben ihre eigenen Regeln, wie man die Tabellen und Beziehungen unter ihnen gestalten sollte.

Die Zielsetzung der Theorie deckt sich mit unserer Zielsetzung, Redundanzen und Konsistenzfehler in den Daten zu vermeiden. Dazu dienen in der relationalen Theorie die Regeln der Normalisierung, die wir uns gleich anschauen werden. Durch die Anwendung der Regeln der Normalisierung wird das Datenmodell in Normalformen gebracht und die Redundanzen und die sich daraus ergebende Gefahr von Inkonsistenzen vermieden.

Im vorhergehenden Abschnitt haben wir uns mit den Abbildungsregeln zwischen der Welt der Objekte und der relationalen Welt beschäftigt. In diesem Abschnitt werden wir uns die Regeln der Normalisierung anschauen und diese in Beziehung zu diesen Abbildungsregeln setzen.

Denormalisierung: Redundanz bewusst einführen

Zunächst aber ein Blick auf die Ausnahme von der Regel. Manchmal gibt es nämlich Gründe, von den Normalformen bei der Datenmodellierung bewusst abzuweichen. Dabei bewegen wir uns bewusst in die entgegengesetzte Richtung und speichern Daten redundant ab, um den Zugriff auf diese Daten zu beschleunigen. Diese Denormalisierung ist eine Möglichkeit, die Effizienz bestimmter Prozesse auf die Kosten anderer Prozesse zu erhöhen.

Nehmen wir zum Beispiel ein Datenmodell, in dem wir eine Tabelle mit Kundendaten vorliegen haben und eine Tabelle mit Bestellungen der Kunden. Die Kunden werden durch die Kundennummer eindeutig identifiziert – die Kundennummer ist ein Primärschlüssel in der Tabelle der Kunden und ein Fremdschlüssel in der Tabelle der Bestellungen.

Wenn wir uns eine Bestellung anschauen möchten, müssen wir beide Tabellen lesen, weil zum Beispiel der Name des Kunden nicht in der Tabelle der Bestellungen, sondern in der Tabelle der Kunden gespeichert wird. Um das Lesen der Kundentabelle beim Anzeigen der Bestellungen zu vermeiden, können wir unser Datenmodell so ändern, dass eine Kopie des Namens des Kunden redundant in der Tabelle der Bestellungen gespeichert wird. Damit soll erreicht werden, dass die Anzeige der Bestellungen schneller erfolgen kann. Diese Beschleunigung wird jedoch durch einen höheren Speicherbedarf für die Tabelle der Bestellungen und erhöhte Komplexität beim Ändern der Kundennamen erkauft.

Normalisierungsregeln und Abbildungsregeln

Wir erwarten, dass die Anwendung der Normalisierungsregeln zu ähnlichen Ergebnissen führt, wie die von uns aufgestellten Regeln der Abbildungen von Klassen auf Tabellen. Schauen wir uns jetzt die Normalformen und die Probleme, die sie lösen, an, und überprüfen wir, ob unsere Abbildungsregeln zu normalisierten Datenmodellen führen.

6.4.1 Die erste Normalform: Es werden einzelne Fakten gespeichert 

Erste Normalform (1NF)

Eine Tabelle ist in der ersten Normalform, wenn in jedem ihrer Felder nur einzelne Werte enthalten sind.

Die erste Normalform definiert eigentlich nur, womit sich die relationale Theorie überhaupt befasst – mit den Relationen über den Wertemengen. Sie besagt, dass wir in jedem Feld einer Tabelle einen einzelnen Wert speichern sollten und nicht eine Liste oder eine Kombination von Werten. Wenn wir also in einer Tabelle die Relation (Land, Stadt) beschreiben wollen, besagt die erste Normalform, dass wir dazu eine Tabelle brauchen, die zwei Spalten hat. In einem Feld eines Datensatzes wird immer maximal ein Land, in dem anderen maximal eine Stadt gespeichert.

In einem Land können jedoch mehrere Städte liegen. Es entspräche nicht der ersten Normalform, wenn wir ein einem Feld eines Datensatzes eine ganze Liste von Städten speichern würden:

Land	Stadt
Deutschland	Berlin, Bonn, Hamburg
Österreich	Wien, Linz, Graz
Italien	Rom, Venedig, Milano

Um das Datenmodell in die erste Normalform zu überführen, muss man die Städte in separaten Datensätzen speichern:

Land	Stadt
Deutschland	Berlin
Deutschland	Bonn
Deutschland	Hamburg
Österreich	Wien
…	…

Einzelwerte und Kombinationen

Was jedoch ein einzelner Wert und was eine Kombination aus Werten ist, ist eine fachliche Entscheidung. Wie schon oben besprochen, kann zum Beispiel eine Postleitzahl ein fachlich relevanter Wert sein, oder sie kann als Bestandteil der Adresse betrachtet werden.

Ein Polygon wird durch die Koordinaten seiner Eckpunkte beschrieben, sind die Werte der Koordinaten einzelne Werte oder kann der ganze Pfad als ein Wert betrachtet werden? Das sind Entscheidungen, die für jede Anwendung getroffen werden müssen. Ist die Relation, die wir in einer Tabelle speichern möchten, die Relation (Kunde, Adresse) oder die Relation (Kunde, Postleitzahl, Straßenname, Hausnummer, Stadt)? Betrachten wir die Polygone als die Relation (ID, Liste der Eckpunkte) oder (ID, Eckpunktnummer, X, Y)?

Diskussion: Abbildungsregeln und erste Normalform

Bernhard: Wie sieht es aber aus, wenn ich eine Liste von Werten zwar nicht in einem Feld eines Datensatzes speichere, sondern mehrere Spalten des gleichen Typs erstelle? Was ist, wenn ich zu einem Kunden maximal drei Telefonnummern speichern möchte und deswegen drei Spalten Telefonnummer1, Telefonnummer2 und Telefonnummer3 definiere?

Gregor: Auch das wäre eine Verletzung der ersten Normalform, wenn die beschriebene Relation (Kunde, Telefonnummer) wäre. Hätten die drei Telefonnummern jedoch unterschiedliche Rollen, so dass man sie nicht beliebig austauschen könnte, wäre es etwas anderes. Eine solche Relation könnte zum Beispiel die folgende sein: (Kunde, Telefonnummer, Faxnummer, Pagernummer)

Bernhard: Aber oben beschreibst Du genau diese Vorgehensweise als eine Möglichkeit, eine 1:n-Beziehung abzubilden. Widersprechen die Mappingregeln denn bereits der ersten Normalform?

Gregor: In der Tat würde eine solche Abbildung einer 1:n-Beziehung der ersten Normalform widersprechen. Daher benutzt man sie auch sehr selten. Sie kann jedoch – als eine Maßnahme der Denormalisierung – sinnvoll sein.

6.4.2 Die zweite Normalform: Alles hängt vom ganzen Schlüssel ab 

Zweite Normalform (2NF)

Eine Tabelle ist dann in der zweiten Normalform, wenn sie in der ersten Normalform ist und alle Werte der Spalten, die nicht ein Teil des Schlüssels sind, funktional von dem gesamten Primärschlüssel abhängig sind.

Wenn ein Primärschlüssel aus mehreren Spalten besteht, sollte keine Untermenge der Primärschlüsselspalten ausreichen, um einen Wert einer anderen Spalte bestimmen zu können.

Nehmen wir als Beispiel eine Tabelle, in der wir die Lieferanten unserer Produkte speichern. Ein Lieferant kann mehrere Produkte liefern, und ein Produkt kann von mehreren Lieferanten zu unterschiedlichen Konditionen geliefert werden.

Wenn wir die Relation (Produkt-Id, Lieferanten-Id, Produktname, Lieferantenname, Preis, Lieferzeit) [In den Fällen, in denen diese Information relevant ist, werden wir die Schlüsselspalten einer Relation unterstrichen darstellen. ] betrachten, stellen wir fest, dass der Produktname sich bereits aus der ID des Produktes bestimmen lässt und der Lieferantenname aus der ID des Lieferantennamens. Nur für den Preis und die Lieferzeit brauchen wir den gesamten Primärschlüssel.

Lieferbedingungen
Produkt-Id	Lieferanten-Id	Produktname	Lieferantenname	Preis	Lieferzeit
1	1	Blumenerde	Garden&Co	10	1
1	2	Blumenerde	Zilinsky und Partner	8	2
2	1	Spaten	Garden&Co	17	1

Verletzung der zweiten Normalform

Dieses Datenmodell entspricht also nicht der zweiten Normalform, und in unseren Daten bestehen Redundanzen. Der Name des Produktes 1 (Blumenerde) wird an mehreren Stellen gespeichert, so wie auch der Name des ersten Lieferanten.

Änderungsanomalien

Wenn wir den Namen des Produktes ändern, müssen wir es entweder in allen Datensätzen ändern, oder unser Datenbestand wird inkonsistent. Dieses Fehlverhalten wird auch als Änderungsanomalie bezeichnet (Update Anomaly).

Um unser Datenmodell in die zweite Normalform zu überführen, müssen wir die Relation aufspalten. Wir überführen die Spalten, die nur von Teilen des Primärschlüssels abhängig gewesen sind, in ihre separaten Relationen. Die Teile des ursprünglichen Primärschlüssels werden jetzt zusätzlich zu Fremdschlüsseln in den neuen Tabellen. Unsere bisherige Tabelle hat also zwei Spalten verloren:

Lieferbedingungen
ProdId	LieferId	Preis	Lieferzeit
1	1	10	1
1	2	8	2
2	1	17	1

Die zugehörigen Daten werden jetzt in zwei separaten Tabellen gespeichert und sind damit nicht mehr redundant. Die Produkte haben ihre eigene Tabelle, ebenso die Lieferanten.

Produkte
ProdId	Produkt
1	Blumenerde
2	Spaten

Lieferanten
LieferId	Lieferant
1	Garden&Co
2	Zilinsky und Partner

2NF und Abbildungsregeln

Objektrelationale Abbildungsregeln und 2NF

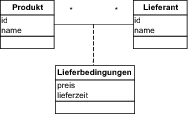
Würden unsere Abbildungsregeln zum gleichen Ergebnis führen wie die Normalisierung? Schauen wir uns das dazugehörige Klassenmodell an, das in Abbildung 6.12 dargestellt ist. In diesem Klassenmodell sehen wir zwei Klassen, die in einer n:m-Assoziation mit einer Assoziationsklasse stehen. Unsere Mappingregeln besagen, dass wir eine n:m-Assoziation durch eine Assoziationstabelle abbilden, die Fremdschlüssel zu den Klassentabellen enthält. Die Attribute der Assoziationsklasse werden dabei in der Assoziationstabelle gespeichert. Und das wäre genau das Datenmodell, das wir durch die Normalisierung erhalten. Damit entspricht die zweite Normalform den Abbildungsregeln für n:m-Beziehungen.

Abbildung 6.12    Klassenmodell – Produkt und Lieferant

6.4.3 Die dritte Normalform: Keine Abhängigkeiten unter den Nichtschlüssel-Spalten 

Die dritte Normalform beschäftigt sich nun mit Spalten, die nicht zum Primärschlüssel gehören.

Dritte Normalform (3NF)

Eine Tabelle ist in der dritten Normalform, wenn sie in der zweiten Normalform ist und keine funktionalen Abhängigkeiten unter den Spalten, die nicht zum Primärschlüssel gehören, bestehen.

Stellen wir uns vor, dass wir bei jeder Bestellung die Kundennummer und den Kundennamen speichern, wie in der unten stehenden Tabelle dargestellt.

Bestellung
Bestellnummer	Kundennummer	Kundenname	Lieferdatum
123456	9876	Anna Müller	11.07.2006
123457	7346	Bertha Maier	14.08.2006
123458	9876	Anna Müller	03.12.2006

Diese Tabelle ist in der ersten und in der zweiten Normalform, denn alle Fakten werden einzeln gespeichert, und die Werte der Nichtschlüssel-Spalten lassen sich aus dem ganzen, und zwar nur dem ganzen, Primärschlüssel bestimmen. Der Primärschlüssel besteht ja nur aus der Spalte Bestellnummer.

Trotzdem haben wir in unserem Datenmodell eine Redundanz, denn es besteht eine funktionale Abhängigkeit zwischen der Kundennummer und dem Kundennamen. Ändern wir den Namen des Kunden in der Bestellung 123456, müssen wir den Namen auch in der Bestellung 123458 ändern. Sonst hätten wir inkonsistente Daten bezüglich der Kundin mit der Kundennummer 9876.

Aufspaltung der Tabelle

Um das Datenmodell in die dritte Normalform zu bringen, müssen wir die Tabelle aufspalten:

Bestellung
Bestellnummer	Kundennummer	Lieferdatum
123456	9876	11.07.2006
123457	7346	14.08.2006
123458	9876	03.12.2006

Kunde
Kundennummer	Kundenname
9876	Anna Müller
7346	Bertha Maier

Die dritte Normalform sagt eigentlich, dass wir in einer Relation Fakten über unterschiedliche Dinge in unterschiedlichen Tabellen speichern sollten; Fakten über Bestellungen in der Tabelle Bestellungen, Fakten über Kunden in der Tabelle Kunden.

Ist eine Tabelle in der dritten Normalform, sind alle Felder eines Datensatzes abhängig vom Primärschlüssel, dem ganzen Primärschlüssel und nichts als dem Primärschlüssel.

Objektrelationale Abbildungsregeln und 3NF

Und was sagen unsere Abbildungsregeln zu dieser Situation? Sie sagen, dass wir eine 1:n-Beziehung so speichern sollen, dass der Primärschlüssel des 1–Teilnehmers in die Tabelle des n-Teilnehmers als Fremdschlüssel hinzugefügt werden kann. Dies entspricht genau unserem normalisierten Datenmodell.

Da die dritte Normalform sich nicht zu den Schlüsselkandidaten äußert, gibt es Fälle, in denen diese trivialerweise erfüllt ist, nämlich dann, wenn alle Spalten einer Tabelle Schlüsselkandidaten sind. Das sich auch hier Redundanzen ergeben können, springt die Boyce-Codd-Normalform ein, um auch dafür Regeln festzulegen.

Die Boyce-Codd-Normalform (BCNF)

Eine Tabelle ist in der Boyce-Codd-Normalform, wenn sie in der dritten Normalform ist und die Teile der Schlüsselkandidaten nicht von Teilen anderer Schlüsselkandidaten funktional abhängig sind.

Wir verdeutlichen diese Definition am besten anhand eines Beispiels.

Spezialist ® Thema

Nehmen wir an, wir betreiben eine Beratungshotline, die zu verschiedenen Themen registrierte Kunden beraten kann. Wir beschäftigen viele Spezialisten, jeder Spezialist ist für genau ein Thema zuständig, für ein Thema haben wir aber mehrere Spezialisten. Es besteht also eine funktionale Abhängigkeit Spezialist ® Thema.

(Kunde, Thema) ® Spezialist

Um die Qualität unserer Dienstleistung zu erhöhen, haben wir beschlossen, dass jeder registrierte Kunde für die Themen, für die er unsere Dienste bestellt hat, immer genau einen Spezialisten als Ansprechpartner haben wird. Es besteht also eine funktionale Abhängigkeit (Kunde, Thema) ® Spezialist.

Die Tabelle, die diese Beziehungen abbildet, sieht zunächst so aus:

Beratungsabos
Kunde	Thema	Spezialist
Alice Müller	Hedge Fonds	Gordon Gekko
Alice Müller	Industrieaktien	James Taggart
Bob Smith	Hedge Fonds	Bud Fox
Christine Neumann	Hedge Fonds	Gordon Gekko
Christine Neumann	Edelmetalle	Francisco d’Anconia

In dieser Tabelle haben wir zwei mögliche Schlüsselkandidaten: Wir können jeden Datensatz mit dem Paar (Kunde, Thema), den wir als den Primärschlüssel gewählt haben, eindeutig bestimmen. Als ein Alternativschlüssel könnte aber auch das Paar (Kunde, Spezialist) dienen. Hätten wir allerdings das Paar (Kunde, Spezialist) als Primärschlüssel gewählt, würde unsere Tabelle nicht die zweite Normalform erfüllen, weil dann die Nichtschlüssel-Spalte Thema von dem Teilschlüssel Spezialist funktional abhängig wäre.

Triviale Erfüllung der 3NF

Da aber unser gewählter Primärschlüssel aus den Spalten (Kunde, Thema) besteht, erfüllt unsere Tabelle sogar die dritte Normalform. Dies ist allerdings in diesem Fall eine triviale Feststellung, da wir nur eine Spalte haben, die nicht zum Schlüssel gehört. Deshalb ist die Erfüllung der dritten Normalform hier keine besonders große Leistung unseres Datenmodells.

Anomalien

Dennoch weist unsere Tabelle ähnliche Anomalien auf wie Tabellen, die nicht in der zweiten Normalform sind. Der Fakt, dass Gordon Gekko sich bei uns auf Hedge Fonds spezialisiert hat, ist redundant gespeichert, und die Daten von Eddie Willers, unserem neuen Spezialisten für Industrieaktien, können wir nicht speichern, weil es noch keinen Kunden gibt, dessen Ansprechpartner er wäre.

Um unser Datenmodell in die BCNF zu überführen, spalten wir die Relation (Kunde, Thema, Spezialist) in zwei neue Relationen (Kunde, Spezialist) und (Spezialist, Thema) auf.

Beratungsabos
Kunde	Spezialist
Alice Müller	Gordon Gekko
Alice Müller	James Taggart
Bob Smith	Bud Fox
Christine Neumann	Gordon Gekko
Christine Neumann	Francisco d’Anconia

Spezialisierungen
Spezialist	Thema
Gordon Gekko	Hedge Fonds
James Taggart	Industrieaktien
Bud Fox	Hedge Fonds
Francisco d’Anconia	Edelmetalle
Eddie Willers	Industrieaktien

Diese Tabellen weisen nun keine Anomalien auf, Gordons Qualifikation wird eindeutig gespeichert, und wir können jetzt auch einen Datensatz für Eddie Willers einfügen. Allerdings wird in dieser Struktur die Einschränkung, dass ein Kunde pro Thema nur einen Ansprechpartner haben darf, nicht durch die Primärschlüssel erzwungen.

Die Herkunft des Namens Boyce-Codd-Normalform

Die bisher betrachteten Normalformen waren sauber durchnummeriert und somit als aufeinander aufbauend erkennbar. Warum heißt also die Boyce-Codd-Normalform nicht einfach vierte Normalform? Die Normalformen wurden in den 70er-Jahren des 20. Jahrhunderts entwickelt, bevor die relationalen Datenbanken breiten Einsatz in der Industrie gefunden hatten. Es gab fünf definierte Normalformen. Erst mit der Verbreitung der relationalen Datenbanken wurde dann erkannt, dass eine Spezialform der dritten Normalform eine Normalform für sich ist. Um eine konsistente Nummerierung der Normalformen beizubehalten, hätte man nun die vierte und fünfte Normalform um einen Platz verschieben müssen. Aus verständlichen Gründen wurde das unterlassen. Daher trägt die Boyce-Codd-Normalform den Namen ihrer Entwickler: Ray Boyce und Edgar Codd.

6.4.4 Die vierte Normalform: Trennen unabhängiger Relationen 

Vierte Normalform

Eine Tabelle ist dann in der vierten Normalform, wenn sie in der Boyce-Codd-Normalform ist und maximal eine nichttriviale mehrwertige, funktionale Abhängigkeit enthält.

Während die vorherigen Normalformen Anomalien behandelten, die von Abhängigkeiten der Felder innerhalb eines Datensatzes herrührten, befasst sich die vierte Normalform mit den Anomalien, die mit Abhängigkeiten zwischen verschiedenen Datensätzen zusammenhängen.

Schauen wir uns die Problemstellung am besten wieder an einem Beispiel an.

Nehmen wir an, die Mitarbeiter unserer Firma sprechen verschiedene Sprachen und haben verschiedene Qualifikationen, die in einer Tabelle Mitarbeiterausbildung enthalten sind.

Mitarbeiterausbildung
Mitarbeiter	Sprache	Qualifikation
Anna	Deutsch	Java
Anna	Englisch	C++
Anna	Englisch	SQL
Bob	Deutsch	Java
Bob	Englisch	C++
Bob	Russisch	C++

BCNF erfüllt

Die Tabelle erfüllt die BCNF, denn es besteht kein Zusammenhang zwischen der Qualifikation eines Mitarbeiters und den Sprachen, die er beherrscht. Aber aus genau diesem Grund enthält unsere Tabelle redundante Daten. Um die Tatsache zu speichern, dass Anna SQL kann, müssen wir auch einen Wert in die Primärschlüsselspalte Sprache eintragen. Da Anna aber außer Deutsch und Englisch keine weitere Sprache spricht, müssen wir entweder Deutsch oder Englisch noch einmal eintragen. Ähnlich sieht es mit Bobs Russischkenntnissen und dem redundant gespeicherten Fakt aus, dass er C++ kann.

Um diese Redundanzen zu beseitigen, könnten wir eine Hilfsspalte zum Primärschlüssel hinzufügen und die nicht benötigten Felder in den Spalten Sprache und Qualifikation leer lassen. Die angepasste Tabelle sieht dann wie folgt aus.

Mitarbeiterausbildung
Mitarbeiter	Zeilennummer	Sprache	Qualifikation
Anna	1	Deutsch	Java
Anna	2	Englisch	C++
Anna	3		SQL
Bob	1	Englisch
Bob	2	Russisch
Bob	3	Deutsch
Bob	4	Deutsch	Java
Bob	5		C++

Doch dies ist keine Lösung, denn auch wenn wir jetzt keine Daten redundant speichern müssen, wir können es immer noch tun. Außerdem gibt es in dieser Datenbankstruktur keine Regel, die bestimmt, wie wir die Daten speichern sollen. Warum speichern wir zum Beispiel Annas Deutschkenntnisse zusammen mit ihrer Qualifikation in Java?

Aufspaltung der Relation

Um die vierte Normalform zu erfüllen, müssen wir die Relation (Mitarbeiter, Sprache, Qualifikation) aufspalten. Da es keinen Zusammenhang zwischen der Sprache und der Qualifikation gibt, können wir zwei neue Relationen definieren: (Mitarbeiter, Sprache) und (Mitarbeiter, Qualifikation).

Es entstehen die neuen Tabellen Sprachkenntnisse und Qualifikationen.

Sprachkenntnisse
Mitarbeiter	Sprache
Anna	Deutsch
Anna	Englisch
Bob	Deutsch
Bob	Englisch
Bob	Russisch

Qualifikationen
Mitarbeiter	Qualifikation
Anna	Java
Anna	C++
Anna	SQL
Bob	Java
Bob	C++

Objektrelationale Abbildungsregeln und 4NF

Wenn wir uns nach unseren objektrelationalen Abbildungsregeln richten, ist es nur selbstverständlich, dass wir für verschiedene n:m-Beziehungen auch verschiedene Assoziationstabellen erzeugen. Durch die Befolgung der Abbildungsregeln droht uns also nicht die Verletzung der vierten Normalform.

6.4.5 Die fünfte Normalform: Einfacher geht’s nicht 

Fünfte Normalform

Eine Tabelle ist dann in der fünften Normalform, wenn sie in der vierten Normalform ist und sie sich nicht ohne Informationsverlust in mehrere Tabellen aufspalten lässt.

Unsere Beispieltabelle Mitarbeiterausbildung aus dem vorhergehenden Abschnitt erfüllte die vierte Normalform nicht, weil in ihr Informationen über unabhängige Tatsachen gespeichert wurden – über die Fremdsprachenkenntnisse und über die Qualifikationen der Mitarbeiter.

Die Forderung der fünften Normalform ist es nun, dass wir eine Tabelle, die verschiedene mehrwertige Tatsachen speichert, nicht mehr weiter zerlegen können, ohne dass wir dadurch relevante Information verlieren. Zur Erinnerung: Mehrwertige Tatsachen sind solche, die durch mehrere Einträge in der Tabelle repräsentiert werden, also zum Beispiel die Tatsache, dass ein Mitarbeiter sowohl Java als auch C++ als Qualifikation aufweist.

Erfüllung der 5NF

Zur Abwechslung zeigen wir diesmal ein Beispiel, das die fünfte Normalform erfüllt. Schauen wir uns die Tabelle Projektqualifikationseinsatz an, in der wir die eingesetzten Qualifikationen unserer Mitarbeiter in verschiedenen Projekten speichern.

Projektqualifikationseinsatz
Mitarbeiter	Projekt	Eingesetzte Qualifikation
Anna	Carmina	C++
Anna	Carmina	SQL
Anna	S-Tool	Java
Anna	S-Tool	SQL
Bob	Carmina	C++
Bob	S-Tool	Java
Chris	S-Tool	C++

Wenn eine Relation nicht in der zweiten, der dritten, der Boyce-Codd- oder der vierten Normalform ist, können wir diese Relation immer in einfachere Relationen zerlegen. Unsere Tabelle Projektqualifikationseinsatz ist in der vierten Normalform, weil die Information über den Projekteinsatz und die eingesetzte Qualifikation nicht voneinander unabhängig sind.

In unserem vorherigen Beispiel zur Tabelle Mitarbeiterausbildung konnten wir die Datensätze (Anna, Deutsch, Java) und (Anna, Englisch, C++) durch (Anna, Deutsch, C++) und (Anna, Englisch, Java) ersetzen, ohne die gespeicherten Tatsachen zu ändern. Bei der Qualifikation im Projekteinsatz können wir jetzt aber gerade nicht die Einträge (Anna, Carmina, Java) und (Anna, S-Tool, C++) durch (Anna, Carmina, C++) und (Anna, S-Tool, Java) ersetzen. Schließlich programmierte Anna im Projekt Carmina in C++ und nicht in Java.

Relation zerlegbar?

Können wir aber die Relation Projektqualifikationseinsatz in einfachere Relationen so zerlegen, dass wir die ursprünglichen Informationen rekonstruieren können? In diesem Fall würde die fünfte Normalform von uns fordern, diese Zerlegung auch vorzunehmen.

In der Relation Projektqualifikationseinsatz speichern wir drei Tatsachen:

• Wer ist an welchem Projekt beteiligt?

• Wer setzt welche Qualifikation ein?

• Welche Qualifikation wird in welchem Projekt eingesetzt?

Schauen wir uns die drei entsprechenden Relationen an. In der Tabelle Projekteinsatz speichern wir, wer an welchem Projekt mitgearbeitet hat.

Tabelle Projekteinsatz

Projekteinsatz
Projekt	Mitarbeiter
Carmina	Anna
Carmina	Bob
S-Tool	Anna
S-Tool	Bob
S-Tool	Chris

Die Tabelle Mitarbeiterqualifikation beschreibt, wer welche Qualifikation eingesetzt hat.

Tabelle Mitarbeiterqualifikation

Mitarbeiterqualifikation
Mitarbeiter	Qualifikation
Anna	Java
Anna	C++
Anna	SQL
Bob	C++
Bob	Java
Chris	C++

Tabelle Projektanforderungen

Schließlich speichern wir in der Tabelle Projektanforderungen, in welchem Projekt welche Qualifikation eingesetzt wurde.

Projektanforderungen
Projekt	Qualifikation
Carmina	C++
Carmina	SQL
S-Tool	Java
S-Tool	SQL
S-Tool	C++

Rekonstruktion der Relation

Können wir aus diesen drei Relationen unsere ursprüngliche Relation Projektqualifikationseinsatz rekonstruieren? Wenn wir die drei einfacheren Relationen kombinieren, bekommen wir folgende Daten.

Projektqualifikationseinsatz rekonstruiert
Mitarbeiter	Projekt	Eingesetze Qualifikation
Anna	Carmina	C++
Anna	Carmina	SQL
Anna	S-Tool	Java
Anna	S-Tool	SQL
Anna	S-Tool	C++
Bob	Carmina	C++
Bob	S-Tool	Java
Bob	S-Tool	C++
Chris	S-Tool	C++

Um aus unseren zerlegten Relationen die ursprüngliche Relation rekonstruieren zu können, müssen wir davon ausgehen, dass jeder im Projekt eingesetzte Mitarbeiter in dem Projekt auch alle seinen vorhandenen und benötigten Qualifikationen einsetzt. Und da im Projekt S-Tool C++ benötigt wird und Anna und Bob zu den S-Tool-Mitarbeitern gehören und C++ können, müssen wir davon ausgehen, dass sie C++ auch im Projekt S-Tool eingesetzt haben.

Rekonstruktion ist nicht möglich.

Nun, das ist nicht der Fall. Im Projekt S-Tool arbeiteten Anna und Bob nur in Java und SQL, um die nötigen C++-Teile kümmerte sich nur Chris.

Die fünfte Normalform fordert von einer Relation, dass sie sich nicht in einfachere Relationen zerlegen lässt, aus denen es möglich wäre, sie wieder zu rekonstruieren. Unsere Relation Projektqualifikationseinsatz ist also in der fünften Normalform.

Diskussion: Firmenpolitik und Normalformen

Bernhard: Und was wäre, wenn wir unsere Firmenpolitik ändern und von unseren Mitarbeiter erwarten würden, dass sie in jedem Projekt, in dem sie benötigt werden, alle ihre Qualifikationen einsetzen?

Gregor: Dann wäre unsere Tabelle nicht in der fünften Normalform, weil sie entweder redundante Daten speichern würde, oder es wäre nicht eindeutig, wie die Daten gespeichert werden sollten. Und wir könnten die Relation so zerlegen, wie wir es getan haben.

Bernhard: Und wenn wir es nur in bestimmten Projekten oder nur bei bestimmten Qualifikationen verlangen würden? Sagen wir, im Projekt Carmina muss jeder alles geben, im Projekt S-Tool nur von ihm explizit verlangte Qualifikationen?

Gregor: In dem Falle müsste unsere Relation auch redundante Daten speichern müssen, oder es wäre nicht eindeutig, wie die Daten gespeichert werden sollen. Allerdings wäre es auch nicht möglich, die Relation rekonstruierbar zu zerlegen, sie wäre also in der fünften Normalform.

Bernhard: Die fünfte Normalform reicht also nicht aus, um redundante Daten und Anomalien des Datenmodells zu beseitigen?

Gregor: Nein, sie reicht nicht. Um diese Anomalien und Redundanzen zu beseitigen, müsste man über ein anderes Datenmodell nachdenken. Zum Beispiel könnte man solche Spezialprojekte wie Carmina in einer anderen Relation verwalten, oder man müsste mit solchen Redundanzen leben. Aber die aufgeführten Normalformen beseitigen nicht alle Redundanzen und Anomalien.

Bernhard: Gibt es noch andere Normalformen, die uns weiterhelfen können?

Gregor: Nein. Durch die Normalisierung kann man die meisten Redundanzen und Anomalien zwar beseitigen, nicht aber alle.

---

Ihre Meinung

Wie hat Ihnen das Openbook gefallen? Wir freuen uns immer über Ihre Rückmeldung. Schreiben Sie uns gerne Ihr Feedback als E-Mail an kommunikation@rheinwerk-verlag.de.