22.8 Backtracking

Backtracking ist ein Verfahren, das nach dem Trial-and-Error-Prinzip (Versuch und Irrtum) ausgeführt wird. Damit wird versucht, aus Teillösungen systematisch zu einer Komplettlösung zu kommen. Steht man beispielsweise bei einer Teillösung vor einer Sackgasse, werden einzelne bzw. mehrere Schritte wieder rückgängig gemacht. Gerät man wieder in eine Sackgasse, werden eben nochmals entsprechend viele Schritte zurück gemacht. Dieser Vorgang wird so lange wiederholt, bis man zu einer Lösung des Problems kommt oder feststellen muss, dass es zu diesem Problem keine Lösung gibt.

22.8.1 Der Weg durch den Irrgarten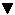

Das Prinzip soll anhand eines simplen Beispiels demonstriert werden. Wir erstellen ein Spielfeld mit Hindernissen (»*«). An der einen Ecke des Spielfeldes befindet sich »Mister C«, der Hunger hat. Auf der anderen Ecke befindet sich etwas zum Essen (»o«). Sie sollen nun mittels Backtracking Mister »C« über die Hindernisse »*« zum Essen »o« führen. Das Ganze sieht folgendermaßen aus:

#################################################
#C *                                            #
#  *                    *                       #
#                                               #
#     *        *   *                        *   #
#            *         *                        #
# *        *   *                 *              #
#                                               #
#   *   *    *       *             *            #
# *                                             #
#           * *                      *          #
#                  *                      *  *  #
#        *       *        *                    o#
#################################################

Das Spielfeld soll mit einem zweidimensionalen char-Array mit 15 Zeilen und 50 Spalten dargestellt werden:

// 15 Zeilen; 50 Spalten
char spielfeld[15][50];

Mister C selbst soll sich erst mal in vier verschiedene Richtungen bewegen können:

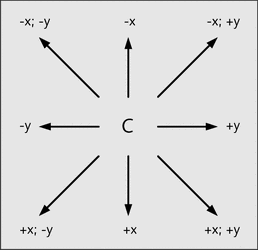
Abbildung 22.37 Koordinatensystem für Mister C

Somit benötigen Sie vier verschiedene Funktionsaufrufe: jeweils einen für die Richtung +x (eine Zeile nach unten), -x (eine Zeile nach oben), +y (eine Spalte nach rechts) und -y (eine Spalte nach links). In der Praxis sehen diese Aufrufe folgendermaßen aus:

step(x, y+1);
step(x+1, y);
step(x-1, y);
step(x, y-1);

Natürlich handelt es sich hierbei um Funktionsselbstaufrufe (Rekursionen). Für die optische Darstellung (Ausgabe des Spielfeldes) sollten Sie hierbei auch noch die alten Positionen von x und y als Argumente bzw. Parameter verwenden:

step(x, y+1, xalt=x, yalt=y);
step(x+1, y, xalt=x, yalt=y);
step(x-1, y, xalt=x, yalt=y);
step(x, y-1, xalt=x, yalt=y);

Als Nächstes müssen Sie bestimmen, in welche Richtung Mister C zuerst gehen soll. Im zweidimensionalen Array gesehen, befindet sich Mister C an Position [1][1] und das Essen an Position [13][48]. Somit können Sie selbst entscheiden, ob Sie zuerst nach rechts (y+1) oder nach unten (x+1) gehen wollen. Im Beispiel wurde die »Verstärkt-nach-rechts-gehen«-Strategie verwendet.

Bevor wir Mister C also nach rechts schicken (y+1), müssen Sie zuerst überprüfen, ob sich in dieser Richtung ein Hindernis (»*«) befindet und ob Sie diese Spalte nicht schon einen Funktionsaufruf zuvor besucht haben (yalt!=y+1). Sind diese beiden Bedingungen erfüllt, können Sie den ersten rekursiven Funktionsaufruf starten (step(x,y+1,x,y)).

Entscheidend für das Backtracking ist nun der Rückgabewert des rekursiven Funktionsaufrufes. Wird 1 zurückgegeben, wird der eben aufgerufene Zug ausgeführt. Hier ist der eben beschriebene Weg »nach rechts«:

if( y+1<49 && spielfeld[x][y+1] !='*' &&
    yalt!=y+1 && step(x,y+1,x,y) )
   return 1;

Die nächsten drei Funktionsaufrufe mitsamt den Überprüfungen sehen recht ähnlich aus, nur dass diese eben für eine andere Richtung bestimmt sind:

else if( x+1<14 && spielfeld[x+1][y] !='*' &&
         xalt!=x+1 && step(x+1,y,x,y))
   return 1;

else if( x-1>0 && spielfeld[x-1][y] !='*' &&
         xalt!=x-1 && step(x-1,y,x,y) )
   return 1;

else if( y-1>0 && spielfeld[x][y-1] !='*' &&
         yalt!=y-1 && step(x,y-1,x,y) )
   return 1;

Falls keiner dieser vier Aufrufe erfolgreich war, wird an den vorangegangenen Funktionsaufruf der Wert 0 (return 0) zurückgegeben, womit eben dieser Zug nicht ausgeführt wird.

Die Abbruchbedingung ist erreicht, wenn sich Mister C an der Position des Essens (»o«) befindet. »Abgebrochen« wird aber auch, wenn das Labyrinth zu komplex ist und unser Mister C partout nicht ans Ziel finden will oder er in einer Sackgasse feststeckt, aus der es kein Zurück mehr gibt. Leider bedeutet dieser Abbruch auch einen Stack-Überlauf. Hierzu die komplette Funktion step():

int step(int x, int y, int xalt, int yalt) {
   printf("<ENTER>");  getchar();
   if(spielfeld[x][y] == 'O') { /* Sind wir am Ziel? */
      spielfeld[x][y] = 'C';
      spielfeld[xalt][yalt] = ' ';
      showspielfeld();
      printf("Mister C ist zu Hause!\n");
      exit (EXIT_SUCCESS);
   }
   else if(spielfeld[x][y] == ' ') {
      spielfeld[x][y] = 'C';
      spielfeld[xalt][yalt] = ' ';
      showspielfeld();
      // ... nach rechts
      if( y+1<49 && spielfeld[x][y+1] !='*' &&
          yalt!=y+1 && step(x,y+1,x,y) )
         return 1;
      // ... nach unten
      else if( x+1<14 && spielfeld[x+1][y] !='*' &&
               xalt!=x+1 && step(x+1,y,x,y) )
         return 1;
      // ... nach oben
      else if( x-1>0 && spielfeld[x-1][y] !='*' &&
               xalt!=x-1 && step(x-1,y,x,y) )
         return 1;
      // ... nach links
      else if( y-1>0 && spielfeld[x][y-1] !='*' &&
               yalt!=y-1 && step(x,y-1,x,y) )
         return 1;
   }
 return 0;
}

Zum besseren Verständnis sollen hier ein paar Durchläufe gemacht werden. Aufgerufen wird die Funktion in main() mit:

step(1,1,1,1);

Somit sieht es auf dem Spielfeld beispielsweise wie folgt aus:

#####################
#C  *
#        *      *
#  *       *       *
#*    *         *

Mister C befindet sich an Position [1][1] im Spielfeld. Zuerst wird in der Funktion step() überprüft, ob er bereits sein Ziel erreicht hat (was im Moment nicht der Fall ist):

if(spielfeld[x][y] == 'O')

Als Nächstes müssen Sie überprüfen, ob die Position [1][1] überhaupt frei ist:

else if(spielfeld[x][y] == ' ' )

Ist diese Position frei, dann kann Mister C dort hingesetzt werden, und es sieht wie in der eben gezeigten Position aus. Jetzt wird überprüft, in welche Richtung Mister C gehen kann:

// ... nach rechts
if( y+1<49 && spielfeld[x][y+1] !='*' &&
    yalt!=y+1 && step(x,y+1,x,y) )

Im Beispiel ist die Richtung y+1 frei und wurde zuvor auch nicht besucht. Somit befindet sich auf dem Stack nun folgender Funktionsaufruf:

step(1, 1+1, 1, 1)

Um ausgeführt zu werden, benötigt dieser Funktionsaufruf ja den Rückgabewert 1. Gehen wir mal ein paar Schritte nach vorn, wo Mister C zum ersten Mal auf ein Hindernis prallt. Folgende Funktionsaufrufe wurden bis dahin getätigt (auf dem Stack von oben nach unten):

step(1,3+1,1,1)
step(1,2+1,1,1)
step(1,1+1,1,1)

Nun sieht das Ganze bildlich folgendermaßen aus:

#####################
#  C*
#        *      *
#  *       *       *
#*    *         *

Hier kommt zum ersten Mal nicht mehr die erste if-Anweisung zum Zuge, da spielfeld[x+1][y] != '*' nicht mehr zutrifft. Die nächste Überprüfung sieht so aus:

// ... nach unten
else if( x+1<14 && spielfeld[x+1][y] != '*' &&
         xalt != x+1 && step(x+1,y,x,y) )

Hier scheint es wieder weiterzugehen. Somit wird als Nächstes eine Zeile nach unten gesprungen, womit sich Mister C an Position [2][3] befindet:

#####################
#   *
# C      *      *
#  *       *       *
#*    *         *

Sie können das Beispiel gern noch ein paar Schritte weiter durchgehen. Mit dem folgenden Beispiel können Sie den Weg von Mister C im echten Leben betrachten:

/* mister_c1.c */
#include <stdio.h>
#include <stdlib.h>
#include <time.h>
#ifdef __unix__
   #define clrscr() printf("\x1B[2J")
#elif __BORLANDC__ && __MSDOS__
   #include <conio.h>
#elif __WIN32__ || _MSC_VER
#define clrscr() system("cls")
#else
   #define clrscr() printf("clrscr() - Fehler!!\n")
#endif

#define HINDERNISSE 100

char spielfeld[15][50];

void createspielfeld(void) {
   int i, j, x, y;
   for(i=0, j=0; j < 50; j++)
      spielfeld[i][j] = '#';

   for(i=1 ;i < 15; i++)
      for(j=0;j<50;j++) {
         if(j==0 || j==49)
            spielfeld[i][j] = '#';
         else
            spielfeld[i][j] = ' ';
         if(i==13 && j==48)
            spielfeld[i][j] = 'O';
      }
      for(i=14,j=0;j<50;j++)
         spielfeld[i][j] = '#';

      for(i=0;i<=HINDERNISSE;i++) {
         x=rand()%14;
         y=rand()%48;
         if(x<15&&y<50 && x>0&&y>0)
            spielfeld[x][y] = '*';

      }
   spielfeld[1][1]=' ';
}

void showspielfeld(void) {
   int i, j;
   clrscr();
   for(i=0; i < 15; i++)
      for(j=0;j<50;j++) {
         printf("%c",spielfeld[i][j]);
         if(j==49)
            printf("\n");
      }
}

int step(int x, int y, int xalt, int yalt) {
   printf("<ENTER>");  getchar();
   if(spielfeld[x][y] == 'O') { /* Sind wir am Ziel? */
      spielfeld[x][y] = 'C';
      spielfeld[xalt][yalt] = ' ';
      showspielfeld();
      printf("Mister C ist zu Hause!\n");
      exit (EXIT_SUCCESS);
   }
   else if(spielfeld[x][y] == ' ') {
      spielfeld[x][y] = 'C';
      spielfeld[xalt][yalt] = ' ';
      showspielfeld();
      /* ... nach rechts */
      if( y+1<49 && spielfeld[x][y+1] !='*' &&
          yalt!=y+1 && step(x,y+1,x,y) )
         return 1;
      /* ... nach unten */
      else if( x+1<14 && spielfeld[x+1][y] !='*' &&
               xalt!=x+1 && step(x+1,y,x,y) )
         return 1;
      /* ... nach oben */
      else if( x-1>0 && spielfeld[x-1][y] !='*' &&
               xalt!=x-1 && step(x-1,y,x,y) )
         return 1;
      /* ... nach links */
      else if( y-1>0 && spielfeld[x][y-1] !='*' &&
               yalt!=y-1 && step(x,y-1,x,y) )
         return 1;
   }
 return 0;
}


int main(void) {
   createspielfeld();
   step(1,1,1,1);
   return EXIT_SUCCESS;
}

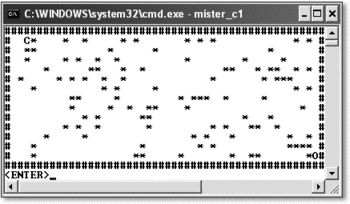
Das Programm bei der Ausführung:

Abbildung 22.38 Mister C auf der Suche nach dem Essen

Dieser Code ist sehr stark auf Rechtsdrang ausgerichtet. Befindet sich Mister C an einer anderen Position, müssen Sie eben das Backtracking den Umständen anpassen.

Wenn Sie im Beispiel die Anzahl der Hindernisse erhöhen, werden Sie merken, dass Mister C irgendwann keinen Ausweg mehr findet, obwohl es rein theoretisch noch welche gibt – sprich, Mister C dreht sich im Kreise. Um dieses Problem zu umgehen, können Sie entweder den Quellcode noch etwas verkomplizieren oder Sie statten Mister C mit weiteren Fähigkeiten aus. Hierfür würde sich beispielsweise eignen, dass sich Mister C auch in die diagonalen Richtungen bewegen kann.

Abbildung 22.39 Mehr Bewegungsfreiheit für Mister C

Somit hätten Sie jetzt folgende vier neue Bewegungen, die Sie in den Code einbauen müssten:

rechtshoch(x-1,y+1)
rechtsrunter(x+1,y+1)
linksrunter(x+1,y-1)
linkshoch(x-1,y-1)

Als Nächstes gilt es auch hier wieder festzulegen, in welcher Reihenfolge diese (jetzt acht) Bewegungen überprüft und ausgeführt werden sollen, um ans Ziel zu kommen. Da sich das Ziel rechts unten befindet, sollten Sie auch wieder diese Richtung als erste Priorität benutzen. Hierfür schlage ich folgenden Weg vor:

if(rechts=frei)
else if(rechtsrunter=frei)
else if(rechtsoben=frei)
else if(nachunten=frei)
else if(linksrunter=frei)
else if(oben=frei)
else if(links=frei)
else if(linksoben=frei)
else return 0

Umgeschrieben auf die Funktion step() sieht dies wie folgt aus:

int step(int x, int y, int xalt, int yalt) {
   printf("<ENTER>");
   getchar();

   if(spielfeld[x][y] == 'O') { /* Sind wir am Ziel? */
      spielfeld[x][y] = 'C';
      spielfeld[xalt][yalt] = ' ';
      showspielfeld();
      printf("Mister 'C' ist zu Hause!\n");
      exit (EXIT_SUCCESS);
   }
   else if(spielfeld[x][y]==' ') {
      spielfeld[x][y]='C';
      spielfeld[xalt][yalt]=' ';
      showspielfeld();
      /* rechts */
      if( y+1<49 && spielfeld[x][y+1] != '*'
          && yalt!=y+1 && step(x,y+1,x,y) )
         return 1;
      /* rechts unten */
      else if( y+1<49 && x+1<14 && spielfeld[x+1][y+1] !='*'
               && xalt!=x+1 && yalt!=y+1 && step(x+1,y+1,x,y) )
         return 1;
      /*rechts oben*/
      else if( x-1>0 && y+1<49 && spielfeld[x-1][y+1]!='*'
               && xalt!=x-1 && yalt!=y+1 && step(x-1,y+1,x,y))
         return 1;
      /* nach unten */
      else if( x+1<14 && spielfeld[x+1][y] !='*'
               && xalt!=x+1 && step(x+1,y,x,y) )
         return 1;
      /* links runter */
      else if(x+1<14 && y-1>0 && spielfeld[x+1][y-1]!='*'
           && xalt!=x+1 && yalt!=y-1 && step(x+1,y-1,x,y))
         return 1;
      /* nach oben */
      else if( x-1>0 && spielfeld[x-1][y] !='*'
               && xalt!=x-1 && step(x-1,y,x,y))
         return 1;
      /* nach links */
      else if( y-1>0 && spielfeld[x][y-1] !='*'
               && yalt!=y-1 && step(x,y-1,x,y))
         return 1;
      /* links oben */
      else if( x-1>0 && y-1>0 && spielfeld[x-1][y-1] !='*'
              && xalt!=x-1 && yalt!=y-1 && step(x-1,y-1,x,y))
         return 1;
  }
  spielfeld[x][y] = ' ';
 return 0;
}

Wenn Sie diese Funktion in das vorige Beispiel einbauen, werden Sie merken, dass Mister C es nun schon mit mehreren Hindernissen aufnehmen kann. Aber ab einer gewissen Anzahl von Hindernissen scheitert Mister C auch hier wieder – und dies, obwohl wir noch nicht in eine Sackgasse gekommen sind.

Also benötigen Sie noch eine Funktion, die sich merkt, ob ein Feld bereits besucht wurde oder nicht. Dies stellt sich als einfaches Unterfangen dar, indem man einfach ein weiteres zweidimensionales Array verwendet:

int besucht[15][50];

Alle Felder werden erst einmal mit dem Wert 0 initialisiert. Im Programmverlauf müssen Sie anschließend nur noch die Position, die bereits besucht wurde, mit dem Wert 1 versehen. Allerdings bedeutet dies auch, dass Sie in jeder Richtung eine weitere Bedingung in der Funktion step() überprüfen müssen.

Hier sehen Sie den kompletten Quellcode mit einem »intelligenten« Mister C:

/* mister_c2.c */
#include <stdio.h>
#include <stdlib.h>
#include <time.h>
#ifdef __unix__
   #define clrscr() printf("\x1B[2J")
#elif __BORLANDC__ && __MSDOS__
   #include <conio.h>
#elif __WIN32__ || _MSC_VER
#define clrscr() system("cls")
#else
   #define clrscr() printf("clrscr() - Fehler!!\n")
#endif

#define HINDERNISSE 200

char spielfeld[15][50];
/* 1=besucht,0=nicht besucht */
int besucht[15][50];

void createspielfeld(void) {
   int i, j, x, y;
   for(i=0, j=0; j < 50; j++)
      spielfeld[i][j] = '#';

   for(i=1 ;i < 15; i++)
      for(j=0;j<50;j++) {
         if(j==0 || j==49)
            spielfeld[i][j] = '#';
         else
            spielfeld[i][j] = ' ';
         if(i==13 && j==48)
            spielfeld[i][j] = 'O';
      }
      for(i=14,j=0;j<50;j++)
         spielfeld[i][j] = '#';

      for(i=0;i<=HINDERNISSE;i++) {
         x=rand()%14;
         y=rand()%48;
         if(x<15&&y<50 && x>0&&y>0)
            spielfeld[x][y] = '*';

      }
   spielfeld[1][1] = ' ';

   for(i=0; i<15; i++)
      for(j=0; j<50; j++)
     besucht[i][j] = 0;
}

void showspielfeld(void) {
   int i, j;
   clrscr();
   for(i=0; i < 15; i++)
      for(j=0;j<50;j++) {
         printf("%c",spielfeld[i][j]);
         if(j==49)
            printf("\n");
      }
}

int step(int x, int y, int xalt, int yalt) {
   printf("<ENTER>");
   getchar();

   if(spielfeld[x][y] == 'O') { /* Sind wir am Ziel? */
      spielfeld[x][y] = 'C';
      spielfeld[xalt][yalt] = ' ';
      showspielfeld();
      printf("Mister 'C' ist zu Hause!\n");
      exit (EXIT_SUCCESS);
   }
   else if(spielfeld[x][y] == ' ') {
      besucht[x][y] = 1;
      spielfeld[x][y]='C';
      spielfeld[xalt][yalt]=' ';
      showspielfeld();
      /* rechts */
      if( y+1<49 && spielfeld[x][y+1] !='*' &&
          yalt!=y+1 &&besucht[x][y+1]!=1 &&
          step(x,y+1,x,y))
         return 1;
      /* rechts unten */
      else if( y+1<49 && x+1<14 && spielfeld[x+1][y+1] !='*'
               && xalt!=x+1 && yalt!=y+1 && besucht[x+1][y+1]!=1
               && step(x+1,y+1,x,y))
         return 1;
      /* rechts oben */
      else if( x-1>0 && y+1<49 && spielfeld[x-1][y+1]!='*'
              && xalt!=x-1 && yalt!=y+1 && besucht[x-1][y+1]!=1
              && step(x-1,y+1,x,y) )
         return 1;
      /* nach unten */
      else if( x+1<14 && spielfeld[x+1][y] !='*'
               && xalt!=x+1 && besucht[x+1][y]!=1
               && step(x+1,y,x,y) )
         return 1;
      /* links unten */
      else if( x+1<14 && y-1>0 && spielfeld[x+1][y-1]!='*'
               && xalt!=x+1 && yalt!=y-1 && besucht[x+1][y-1]!=1
               && step(x+1,y-1,x,y) )
         return 1;
      /* nach oben */
      else if( x-1>0 && spielfeld[x-1][y] !='*'
               && xalt!=x-1 && besucht[x-1][y]!=1
               && step(x-1,y,x,y) )
         return 1;
      /* nach links */
      else if( y-1>0 && spielfeld[x][y-1] !='*'
               && yalt!=y-1 && besucht[x][y-1]!=1
               && step(x,y-1,x,y) )
         return 1;
      /* links oben */
      else if( x-1>0 && y-1>0 && spielfeld[x-1][y-1] !='*'
               && xalt!=x-1 && yalt!=y-1 && besucht[x-1][y-1]!=1
               && step(x-1,y-1,x,y) )
         return 1;
   }
   spielfeld[x][y]=' ';
   return 0;
}

int main(void) {
   createspielfeld();
   step(1,1,1,1);
   return EXIT_SUCCESS;
}

Auch wenn Ihnen das ganze Thema recht komplex erscheinen mag, so entspricht dies doch einem logischen Ablauf. Man muss eben 1 zurückgeben, wenn der Weg, den man probiert hat, ans Ziel führt. Befindet man sich in einer Sackgasse, muss man einen anderen Wert zurückgeben (in diesem Beispiel 0). Außerdem sollte man einen Weg, den man schon einmal gegangen ist, nicht nochmals zurückgehen (da dieser bekanntlich nicht zum Ziel führt). Mit dieser Strategie kommen Sie durch einen beliebig komplexen Irrgarten immer ans Ziel (sofern ein Weg zum Ziel existiert und der Irrgarten nicht so komplex ist, dass es einen Stack-Überlauf gibt).

22.8.2 Das 8-Dame-Problem

Ein etwas weiter verbreitetes Beispiel für das Backtracking ist das 8-Dame-Problem. Die Aufgabe lautet: »Positionieren Sie 8 Damen auf einem Schachbrett so, dass diese sich nicht gefährden.« Für diejenigen, die es nicht wissen: Die Dame kann von ihrer aktuellen Position aus beliebig viele Felder in der gleichen Spalte, in der gleichen Reihe oder in den Diagonalen rücken – was bedeutet, dass in diesen Richtungen keine andere Dame stehen darf. Versuchen Sie es mal auf dem Schachbrett nachzuahmen. Es gibt exakt 92 Möglichkeiten.

Sie haben hierbei die Möglichkeit, ein zweidimensionales Array für das Schachbrett zu verwenden, aber da sich zwei Damen in der gleichen Reihe oder Spalte sowieso bedrohen würden, können Sie sich das ersparen. Da die erste Dame, die Sie setzen, keine Bedrohung zu befürchten hat, setzen wir diese gleich an die rechte obere Ecke. Somit könnte der Funktionsaufruf wie folgt aussehen:

int schachbrett[8];
int i;

for(i = 0; i < 8; i++)
   schachbrett[i] = 0;
/* Dame an die linke obere Ecke */
dame(schachbrett, 7);

Hierzu nun ein Teil der Funktion dame():

int dame(int *schachbrett, int position) {
    int x = 1;
    static int counter = 1;
    while(x<=8) {
       schachbrett[position] = x;

Der Wert x dient zur Identifizierung der einzelnen Damen. Jede Dame bekommt eine Nummer. Des Weiteren dient dieser Wert auch noch zur Überprüfung, ob eine Dame in der Diagonalen gefährdet wird. Aber dazu später mehr. Mit der Zeile

schachbrett[position] = x;

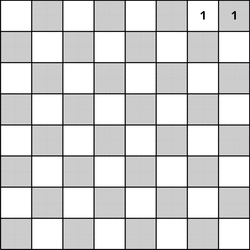
bekommt das Feld 7 (genauer Feld 8, aber da hier 0 ebenfalls als erstes Feld präsent ist, eben 0 bis 7 anstatt 1 bis 8) rechts oben den Wert 1:

Abbildung 22.40 Die erste Dame wurde rechts oben gesetzt (1).

Als Nächstes benötigen Sie eine Funktion, um zu testen, ob die Dame mit der Nummer 1 auf der Reihe, Spalte und Diagonalen mit einer anderen Dame kollidiert:

if(!dame_in_gefahr(schachbrett))

Der Funktion übergeben Sie lediglich die Daten vom Schachbrett. Im ersten Durchlauf wird die Bedingung logischerweise wahr sein – d. h., die Dame ist nicht in Gefahr.

Jetzt müssen Sie überprüfen, ob Sie nicht schon an Position 0 angekommen sind (bildlich wäre das, in einer Spalte ganz unten angekommen zu sein):

if(position)

Falls Sie noch nicht die ganze Spalte durch haben, beginnt ab hier der erste rekursive Aufruf (und eine Erhöhung des Stacks):

// die nächste Dame setzen
if(dame(schachbrett,position-1))
   return 1;

Nochmals die Funktion bis hierher im Überblick:

int dame(int *schachbrett, int position) {
   int x = 1;
   static int counter = 1;

   while(x <= 8) {
      schachbrett[position]=x;
      if(!dame_in_gefahr(schachbrett)) {
         if(position) {
            /* die nächste Dame ... */
            if(dame(schachbrett,position-1))
               return 1;   /* Dame an diese Position setzen */
         }
         else
            return 1;

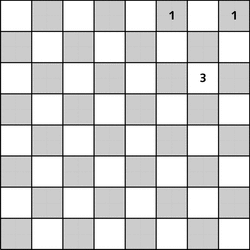
Mit dem erneuten Funktionsaufruf sieht die Situation folgendermaßen auf dem Schachbrett aus:

Abbildung 22.41 Erster rekursiver Funktionsaufruf – eine weitere Dame

Jetzt ist eine Dame an Position 7 in Gefahr, und folgende Bedingung trifft nicht zu:

if(!dame_in_gefahr(schachbrett))

Folglich wird der Zähler x um 1 inkrementiert:

x++;

Bildlich dargestellt, ergibt sich nun durch folgende Code-Zeile folgender Zustand auf dem Schachbrett:

schachbrett[position]=x;

Abbildung 22.42 Ein weiterer Zug der zweiten Dame

Auch in dieser Stellung liegt eine Kollision vor. Also wird x nochmals inkrementiert, womit Sie folgenden Zustand vorfinden:

Abbildung 22.43 Ein weiterer Zug, und es ist keine Kollision mehr vorhanden.

Jetzt gefährden sich beide Damen nicht mehr, und somit wird wieder ein erneuter rekursiver Funktionsaufruf ausgeführt. Der Stand der aktuellen Funktion wird wieder auf den Stack getan (zweite Funktion auf dem Stack) und wartet wiederum auf ihren Einsatz. Jetzt geht das Spiel von Neuem los. Der nächste Schritt sieht bildlich so aus (siehe Abbildung 22.44).

Abbildung 22.44 Der zweite rekursive Funktionsaufruf von »dame()«

Da die Dame in den nächsten drei Reihen sowieso kollidiert, überspringen wir diese drei Schritte, wo jeweils der Wert von x dreimal inkrementiert wird, bis folgende Stellung erreicht wurde:

Abbildung 22.45 Es ist keine Kollision mehr vorhanden.

Wohl gemerkt heißt das noch lange nicht, dass dies die endgültige Stellung darstellt, da alle diese Funktionsaufrufe noch auf dem Stack liegen und darauf warten, was mit ihnen passieren soll (1 = bleibt so; 0 = weitersuchen). Nach weiteren rekursiven Funktionsaufrufen passiert endlich etwas:

Abbildung 22.46 Noch gibt es keine Kollision.

Der nächste Funktionsaufruf (für die erste Spalte) wird nun den Wert 0 zurückgeben, da sich in der ersten Spalte keine Dame platzieren lässt, ohne dass diese sich mit einer anderen gefährdet. Jetzt »trackt« unsere Funktion zur zweiten Spalte »back«.

Der Wert von x, der auf dem Stack gespeichert wurde, betrug in der zweiten Spalte 6, somit wird dieser wieder inkrementiert und es geht in Zeile 7 (zweite Spalte) weiter. Dort findet eine weitere Kollision statt, ebenso wie in der Zeile 8 (zweite Spalte). Somit bekommt auch der Aufrufer der zweiten Spalte den Wert 0 zurück, und unser Programm nimmt seine Ausführung in der dritten Spalte (von links) und der vierten Zeile (Wert von x ist hier 4) wieder auf. Weitere Inkrementierungen in dieser Spalte bringen auch keinen Erfolg, sondern nur weitere Kollisionen.

Dies geht so lange weiter zurück, bis entweder keine Kollision mehr stattfindet (dann geht es wieder »nach vorne« weiter) oder die Bedingung

if(position)

unwahr wird. Das heißt, wir sind am Ende angekommen. Dies wird mit einem return 1 bestätigt:

if(position) {
   if(dame(schachbrett,position-1))
      return 1; //Dame an diese Position setzten
}
else
   return 1;  //Wir sind fertig, wir haben eine Lösung

... oder aber auch, wenn Sie alle 92 Möglichkeiten ausgeben wollen. Wir benutzten Letzteres. Ich empfehle Ihnen, um das ganze Programm besser zu verstehen, es Schritt für Schritt auf einem Schachbrett nachzuspielen.

Hierzu noch das komplette Listing, das das 8-Dame-Problem programmtechnisch auflöst:

/* 8dame.c */
#include <stdio.h>
#include <stdlib.h>

int dame_in_gefahr(int *schachbrett) {
   /* x==nach unten; y==nach rechts */
   int x,y;
   for(x=0; x<7; x++)
      /* Ist auf feld[x] eine Dame? */
      if(schachbrett[x])
      for(y=x+1; y<=7; y++)
         /* Ist auf feld[y] eine Dame? */
         if(schachbrett[y])  {
            /* Wir überprüfen, ob die beiden
             * Damen kollidieren. */
            /* Sind beide Damen in derselben Zeile? */
            if(schachbrett[x]==schachbrett[y])
               return 1; /* Kollision in gleicher Zeile */
            /* Diagonal? */
            if(abs(x-y)==abs(schachbrett[x]-schachbrett[y]))
              return 2; /* Kollision in der Diagonalen */
         }
   return 0; /* keine Kollision! */
}

int dame(int *schachbrett, int position) {
   int x = 1, i;
   static int counter = 1;

   while(x <= 8) {
      /* Wir setzen die Dame mit der
       * Nummer x an feld[position]. */
      schachbrett[position]=x;
      if(!dame_in_gefahr(schachbrett)) {
         if(position) {
            /* die nächste Dame */
            if(dame(schachbrett,position-1))
               return 1; /* Dame an diese Position setzen */
         }
         else {
            printf("Loesungs-Nr.%2d : ", counter++);
            for(i=0; i<8; i++)
               printf("(%d,%d)", i+1, schachbrett[i]);
            printf("\n");
         }
      }
      x++;
   }
   schachbrett[position] = 0;
   return 0;
}

int main(void) {
   int schachbrett[8], x;

   for(x=0; x < 8; x++)
      schachbrett[x] = 0;
   dame(schachbrett,7);
   return EXIT_SUCCESS;
}

In der Zeile

if(abs(x-y)==abs(schachbrett[x]-schachbrett[y]))

wird eine absolute Zahl berechnet, das heißt beispielsweise, der absolute Wert von 2–6 ist 4 und nicht –4. Diese Berechnung und Bedingung dient dazu, zu überprüfen, ob in der Diagonalen eine Kollision mit einer Dame stattfindet.

Hier sehen Sie noch eine der 92 möglichen Lösungen:

Abbildung 22.47 Keine Dame ist gefährdet.

Ihre Meinung

Wie hat Ihnen das Openbook gefallen? Wir freuen uns immer über Ihre Rückmeldung. Schreiben Sie uns gerne Ihr Feedback als E-Mail an kommunikation@rheinwerk-verlag.de.