22.5 Hashing (Zerhacken)

Das Hashing ist eine bekannte Methode zum Suchen und Speichern von Datensätzen mithilfe einer Tabelle, bei der ein Schlüssel in eine Tabellenadresse umgewandelt wird. Durch diese Umwandlung kann bei einer Suche sofort auf diese Tabellenadresse gesprungen werden, ohne den vollständigen Datensatz (bei binärer Suche einen Teil des Datensatzes) zu durchlaufen. Die Ziele beim Hashing sind dabei eine effizientere Nutzung der verfügbaren Speicherkapazität und ein schnellerer Zugriff.

22.5.1 Wann wird Hashing verwendet?

Das beste Beispiel für Hashing sind Symboltabellen, bei denen Werte durch jedes Element mit einer dynamischen Menge von Strings assoziiert werden. So geschieht dies etwa beim Compiler. So kann ein Compiler alle Variablen eines Programms am effizientesten verwalten.

Ein weiteres Beispiel ist die (verräterische) Autovervollständigung des Browsers oder auch der Cache des Webbrowsers, der den Verlauf speichert. Ein simples Beispiel für Hashing ist die Zählung von Wörtern, die in einem Text vorkommen. Abfragen, die auf ein digitales Wörterbuch angewendet werden, können mit Hashing ebenso effizient gestaltet werden wie die Programmierung von großen Datenbanken. Denn in diesen Fällen ist es wirklich geboten, unglaublich viele Daten in kurzer Zeit zu durchsuchen.

22.5.2 Was ist für das Hashing erforderlich?

• Eine Hash-Funktion – mit der Hash-Funktion wird eine eindeutige Adresse erzeugt, die die Position des Datensatzes in der Hash-Tabelle bestimmt.

• Eine Hash-Tabelle – in der Hash-Tabelle befinden sich die eindeutigen Adressen. Eine Suchanfrage wird zunächst mit der Hash-Funktion in eine Tabellenadresse umgewandelt. Mit dieser eindeutigen Adresse wird im Anschluss der Datensatz in der Hash-Tabelle gesucht.

Die Hash-Funktion wird in der Praxis meist mit einem Array passender Größe angegeben, das zur Kompilierzeit angelegt wird. Einfach ausgedrückt: Eine Hash-Tabelle mit 10 Elementen ist ein Array mit verketteten Listen – mit der Größe von 10 * Arraygröße. In jedem Index dieses Arrays könnte eine verkettete Liste sein.

Das soll jetzt in der Praxis untersucht werden. Hier wird wieder das Postleitzahlen-Beispiel verwendet:

struct plz{
   char ort[MAX];
   unsigned int postleit;
   struct plz *next;
};

Die Hash-Tabelle, die jetzt für die verkettete Liste verwendet wird, sieht wie folgt aus:

struct plz *hash_tabelle[MAX_HASH];

Um es einfach zu halten, wird eine niedrige Arraygröße verwendet:

#define MAX_HASH 10

Abbildung 22.25 zeigt die aktuelle Hash-Tabelle in grafischer Dargestellung:

Abbildung 22.25 Leere Hash-Tabelle

Jetzt benötigen Sie eine Funktion, um einen neuen Datensatz zum Hash hinzuzufügen:

struct plz *insert(char *o, unsigned int p) {
   struct plz *pointer;
   /* Hash-Wert (bucket) an hash_adresse (0-9) */
   int hash_adresse = hash_funktion(o);

   / *printf("%d\n",hash_adresse); */

   /* Zeiger auf errechnete Tabellenadresse
    * durch hash_funktion */
   pointer = hash_tabelle[hash_adresse];
   /* Wir suchen freien Platz für einen neuen Eintrag
    * in hash_tabelle[hash_adresse] */
   while(pointer != NULL) {
      if(strcmp(o, pointer->ort) == 0)  /* Stadt gleich? */
         if(pointer->postleit == p) {
            /* Postleitzahlen gleich? */
            printf("%s mit PLZ %d ist bereits vorhanden\n",o,p);
            /* doppelte Einträge vermeiden */
            return pointer;
         }
         pointer=pointer->next;
   }

   /* Speicher für neues Element allozieren */
   pointer = malloc(sizeof(struct plz));
   if(pointer == NULL) {
      printf("Kein Speicher für neue PLZ vorhanden\n");
      return NULL;
   }
   strcpy(pointer->ort, o);
   pointer->postleit = p;
   pointer->next = hash_tabelle[hash_adresse];
   hash_tabelle[hash_adresse] = pointer;
   return pointer;
}

Die Funktion wird jetzt Schritt für Schritt erläutert. Wir beginnen mit:

int hash_adresse = hash_funktion(o);

Hiermit bekommt die Variable hash_adresse einen errechneten Hash-Wert, der logischerweise zwischen 0 und 9 liegen muss, da die Hash-Tabelle 10 Slots besitzt. Nehmen wir an, dass der Funktion insert() folgende Werte übergeben wurden:

insert("Augsburg", 86163);

Die Hash-Funktion errechnet in diesem Beispiel aus dem String "Augsburg" den Wert 6. Somit kommt der String "Augsburg" in den Index (Slot) 6 der Hash-Tabelle. Auf diesen Slot soll jetzt erst ein Zeiger verweisen:

 /* Zeiger auf errechnete Tabellenadresse
  * durch hash_funktion */
 pointer = hash_tabelle[hash_adresse];

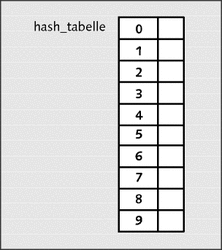
Bildlich sieht dies wie folgt aus:

Abbildung 22.26 Zeiger auf errechneten Index

Jetzt muss ein freier Speicherplatz für die neuen Daten gesucht werden:

   while(pointer != NULL) {
      if(strcmp(o, pointer->ort) == 0)  /* Stadt gleich? */
         if(pointer->postleit == p) {
            /* Postleitzahlen gleich? */
            printf("%s mit PLZ %d ist bereits vorhanden\n",o,p);
            /* Doppelte Einträge vermeiden */
            return pointer;
         }
         pointer=pointer->next;
   }

Im ersten Fall ist dies recht trivial. Also kann der neue Datensatz gleich in die Hash-Tabelle eingefügt werden mit:

 strcpy(pointer->ort, o);
 pointer->postleit = p;
 pointer->next = hash_tabelle[hash_adresse];
 hash_tabelle[hash_adresse] = pointer;

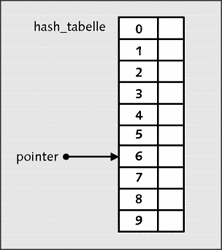
Jetzt befindet sich das erste Element in der Hash-Tabelle. Grafisch dargestellt sieht dies dann so aus:

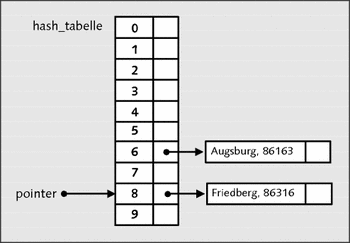
Abbildung 22.27 Ein erster Datensatz wurde hinzugefügt.

Nun folgt ein weiterer Datensatz:

insert("Friedberg", 86316);

Die Hash-Funktion, die Ihnen immer noch vorenthalten wurde, errechnet hierbei den Index (Slot) 8. Darauf sieht die Hash-Tabelle nach dem Abarbeiten der Funktion insert() so aus:

Abbildung 22.28 Ein weiterer Datensatz wurde hinzugefügt.

Kommen wir jetzt zu einem speziellen Fall beim Hashing. Es wird folgender neue Datensatz eingefügt:

insert("Stuttgart", 70190);

Die Hash-Funktion errechnet aus dem String "Stuttgart" den Indexwert 8.

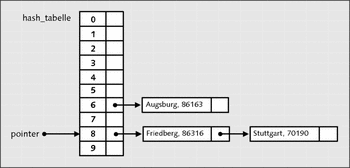
Beim Betrachten der Abbildung 22.29 können Sie erkennen, dass Slot 8 bereits einen Inhalt hat ("Friedberg"). Dies wird Kollision genannt, und es bedeutet, dass die Hash-Funktion zu unterschiedlichen Schlüsseln gleiche Werte liefern kann. Deshalb wurde ja auch eine lineare verkettete Liste verwendet. Somit wird der neue Datensatz einfach hinter "Friedberg" eingefügt. In der Informatik wird dies als Synonymkette bezeichnet.

Abbildung 22.29 Ein Datensatz wurde nach einer Kollision hinzugefügt.

22.5.3 Hash-Funktion

Anhand dieses Beispiels dürfte klar sein, dass der Hash-Funktion eine entscheidende Rolle zufällt. Wie Sie eine solche Funktion schreiben, bleibt Ihnen selbst überlassen. Sie könnten sogar eine Funktion schreiben, die Zufallszahlen zwischen 0 und 9 zurückliefert. Doch was nutzt eine solche Funktion, wenn 90 % der Zufallszahlen zum Beispiel zwischen 2 und 4 liegen? Die restlichen Slots werden dabei kaum verwendet.

Für tatsächlich effektive Hash-Berechnungen existieren drei Methoden:

• Divisionsmethode

• Mittquadratmethode

• Zerlegungsmethode

Divisionsmethode

Für m sollten Sie idealerweise eine Primzahl so nahe wie möglich am höchsten Index wählen.

Mittquadratmethode

I ist key, wobei führende und endende Ziffern entfernt werden müssen. Beispielsweise:

H(3206) = 32062 = 10278436

Von dem Wert 10278436 werden abwechselnd rechts und links die Ziffern abgeschnitten, bis ein Wert entsteht, der kleiner als der Index ist. Wenn z. B. eine Hash-Tabelle mit dem Index 10 deklariert wurde, sieht der Wert aus dem Schlüssel 10278436 wie folgt aus:

1027 [8] 436 = 8

Zerlegungsmethode

Man zerlegt den Schlüssel, bis er eine gültige Adresse hat. Als Beispiel verwenden wir den Schlüssel 135612:

135612 = [13]+[56]+[12]= 81 = [8]+[1] = 9

Der Schlüssel wurde zerlegt, bis er als gültige Adresse den Wert 9 besitzt.

Hashing von Strings

Ein bewährter Hash-Algorithmus für Strings erzeugt einen Hash-Wert, in dem er jedes Byte des Strings zum Vielfachen des Strings hinzuaddiert. Eine Multiplikation verteilt die einzelnen Bits des Bytes auf den bisher berechneten Wert. Tests haben ergeben, dass sich bei Strings die Werte 31 und 37 als gute Multiplikatoren erwiesen haben, die auch für das Programmbeispiel verwendet werden.

Theoretisch könnten Sie sich das Beispiel anhand des Postleitzahlen-Listings so vorstellen. Für String "Stuttgart" wurden die Postleitzahlen 70190 eingetragen:

hash_tabelle["Stuttgart"] = 70190;

Dies ist eigentlich ein Array mit dem Indexwert als String. In der Praxis ist dies in C natürlich nicht möglich. Dafür schreiben Sie ja auch die Hash-Funktion.

Die passende Hash-Funktion für das Programmbeispiel sieht so aus:

/* die Hash-Funktion zur Berechnung des
 * Hash-Werts eines Strings */
int hash_funktion(char *string) {
   unsigned int hash_adresse;
   unsigned char *pointer;

   hash_adresse = 0;
   pointer = (unsigned char *) string;
   while(*pointer != '\0') {
      hash_adresse = M * hash_adresse + *pointer;
      pointer++;
   }
   return hash_adresse % MAX_HASH;
}

Um sicherzustellen, dass auch positive Hash-Adressen für die Hash-Tabelle zurückgeliefert werden, wird unsigned verwendet.

Es ist relativ schwierig, eine optimale Hash-Funktion zu finden. In solch einem Fall müssen Sie so lange testen, bis Sie mit dem Ergebnis zufrieden sind. Hier sehen Sie das vollständige Programm, das das Hashing mit getrennter Verkettung demonstrieren soll:

/* hashing.c */
#include <stdio.h>
#include <string.h>
#include <stdlib.h>
#define MAX_HASH 10
#define M 31

struct plz{
   char ort[255];
   unsigned int postleit;
   struct plz *next;
};

struct plz *hash_tabelle[MAX_HASH];

struct plz *insert(char *, unsigned int);
void search_in_hash(char *);
int hash_funktion(char *);

struct plz *insert(char *o, unsigned int p) {
   struct plz *pointer;
   /* Hash-Wert (bucket) an hash_adresse (0-9) */
   int hash_adresse = hash_funktion(o);

   /* printf("%d\n",hash_adresse); */

   /* Zeiger auf errechnete Tabellenadresse
    * durch hash_funktion */
   pointer = hash_tabelle[hash_adresse];
   /* Wir suchen freien Platz für einen neuen Eintrag
    * in hash_tabelle[hash_adresse] */
   while(pointer != NULL) {
      if(strcmp(o, pointer->ort) == 0)  /* Stadt gleich? */
         if(pointer->postleit == p) {
            /* Postleitzahlen gleich? */
            printf("%s mit PLZ %d ist bereits vorhanden\n",o,p);
            /* doppelte Einträge vermeiden */
            return pointer;
         }
         pointer=pointer->next;
   }
   /* Speicher für neues Element allozieren */
   pointer = malloc(sizeof(struct plz));
   if(pointer == NULL) {
      printf("Kein Speicher für neue PLZ vorhanden\n");
      return NULL;
   }
   strcpy(pointer->ort, o);
   pointer->postleit = p;
   pointer->next = hash_tabelle[hash_adresse];
   hash_tabelle[hash_adresse] = pointer;
   return pointer;
}

/* Funktion zur Suche in der Hash-Tabelle */
void search_in_hash(char *o) {
   struct plz *pointer;
  /* Hash-Wert (bucket) an hash_adresse (0-9) */
   int hash_adresse = hash_funktion(o);

   /* printf("%d\n",hash_adresse); */

   /* Zeiger auf errechnete Tabellenadresse
    * durch hash_funktion */
   pointer = hash_tabelle[hash_adresse];

   /* Jetzt wollen wir nachsehen, ob es für o einen
    * Eintrag in der Tabelle gibt. */
   while(pointer != NULL) {
      if(strcmp(pointer->ort, o) == 0)
         printf("PLZ fuer %s ist %d\n",o,pointer->postleit);
      pointer = pointer->next;
   }
}

/* die Hash-Funktion zur Berechnung des Hash-Werts
 * eines Strings */
int hash_funktion(char *string) {
   unsigned int hash_adresse;
   unsigned char *pointer;

   hash_adresse = 0;
   pointer = (unsigned char *)string;
   while(*pointer != '\0') {
      hash_adresse = M * hash_adresse + *pointer;
      pointer++;
   }
   return hash_adresse % MAX_HASH;
}

int main(void) {
   /* einfügen */
   insert("Friedberg", 86316);
   insert("Augsburg", 86136);
   insert("Stuttgart", 71345);
   /* suchen */
   search_in_hash("Augsburg");
   search_in_hash("Friedberg");
   search_in_hash("Stuttgart");
   return EXIT_SUCCESS;
}

Die Suchfunktion search_in_hash() ist ähnlich wie insert(). Daher erkläre ich sie nicht weiter. Wichtig ist es aber auch, zu erwähnen (auch wenn dies eigentlich logisch sein sollte), dass jede Funktion, die Sie hinzufügen (suchen, sortieren, löschen, einfügen, ...), dieselbe Hash-Funktion verwenden muss.

22.5.4 Hashing mit direkter Adressierung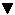

Es ist auch möglich, die einzelnen Hashes direkt zu adressieren, sofern Sie abschätzen können, wie viele Elemente eingefügt werden. Dafür wird eine Tabelle verwendet, die nur Zeiger auf die anderen Stellen im Speicher abgelegter Datensätze enthält. Die direkte Adressierung lässt sich folgendermaßen realisieren (Pseudocode):

while(Schlüssel_stimmt_nicht_überein) {
   if(Schlüssel_stimmt_überein) {
      printf("gefunden");
      return;
   }
   else if(Speicherplatz leer) {
      printf("nicht gefunden");
      return;
   }
   weiter_an_die_nächste_Position;
}

Der Vorteil der direkten Adressierung besteht in der größeren Schnelligkeit. Der große Nachteil ist aber die fixe Tabellengröße. Sofern Sie die Menge der Daten abschätzen können, ist diese kein Nachteil. Bei Datenbanken, bei denen die Menge der Daten vom Anwendungsfall abhängt, ist die direkte Adressierung nicht sinnvoll.

22.5.5 Vergleich von Hashing mit binären Bäumen

Vorteile des Hashings:

• einfach zu implementieren

• schnelle Suchergebnisse

Vorteile binärer Bäume:

• Garantie für Leistungsfähigkeit auch im ungünstigsten Fall

• unterstützt viele weitere Operationen (z. B. das Sortieren)

• dynamisch (Bei binären Bäumen ist im Gegensatz zum Hashing keine Information über die Anzahl der Einfügungen nötig.)

Ihre Meinung

Wie hat Ihnen das Openbook gefallen? Wir freuen uns immer über Ihre Rückmeldung. Schreiben Sie uns gerne Ihr Feedback als E-Mail an kommunikation@rheinwerk-verlag.de.