5.8 Die Gleitpunkttypen »float« und »double« 

Jetzt kommen wir zu den Gleitpunkttypen (Floatingpoint). Mit ihnen wird es möglich, genauere Berechnungen mit Nachkommastellen auszuführen. Hier wieder zuerst eine kleine Übersicht:
| Name | Größe | Wertebereich | Genauigkeit | Formatzeichen |
float |
4 Byte |
1.2E-38 3.4E+38 |
6-stellig |
%f |
double |
8 Byte |
2.3E-308 1.7E+308 |
15-stellig |
%lf |
long double |
10 Byte |
3.4E-4932 1.1E+4932 |
19-stellig |
%Lf |
Beachten Sie, dass die Größenangaben und Wertebereiche dieser Typen komplett implementierungsabhängig sind. Es ist lediglich gewährleistet, dass bei float, double und long double (hier von links nach rechts) jeder Typ den Wert des vorherigen aufnehmen kann.
Angewendet wird dieser Datentyp genauso wie int und alle anderen Datentypen, die Sie bereits kennen.
Hierzu eine kurze Erklärung, warum es Gleitpunkttyp und nicht Gleitkommatyp heißt. Dies liegt daran, dass die Programmiersprache C in den USA entwickelt wurde. Und dort wird anstatt eines Kommas zwischen den Zahlen ein Punkt verwendet (man spricht von floating point variables):
float a=1,5; /* FALSCH */ float b=1.5; /* RICHTIG */
Das Komma verwenden die US-Amerikaner wiederum genauso wie Europäer den Punkt bei größeren Zahlen. Folgendes Beispiel schreiben wir (Europäer) so:
1.234.567
Und die US-Amerikaner schreiben dies wiederum so:
1,234,567
Dazu ein Beispiel. Es wird ein Programm geschrieben, das die Fläche eines Rechtecks berechnet.
/* rectangle.c */
#include <stdio.h>
int main(void) {
/* Deklaration */
float flaeche, l, b;
printf("Berechnung der Flaeche eines Rechtecks\n");
/* Werte einlesen */
printf("Laenge des Rechtecks: ");
scanf("%f",&l);
printf("Breite des Rechtecks: ");
scanf("%f",&b);
/* Fläche berechnen */
flaeche = l * b;
printf("Flaeche des Rechtecks betraegt : %f\n",flaeche);
return 0;
}Bei diesem Listing wird der Anwender nach der Länge und der Breite einer rechteckigen Fläche gefragt. Diese Gleitpunktzahl wird mithilfe von scanf() eingelesen und an die Adressen der Variablen l und b übergeben. Anschließend wird dieser Wert zur Berechnung verwendet. Das Ergebnis wird am Schluss des Programms auf dem Bildschirm ausgegeben.
Beachten Sie im Zusammenhang mit Gleitpunktzahlen auch Folgendes: Wenn Sie zwei verschiedene Variablen z. B. int und float miteinander durch Operatoren verknüpfen, erhalten Sie das Ergebnis vom genaueren Datentyp dieser beiden Variablen zurück. Ein Beispiel:
/* divide.c */
#include <stdio.h>
int main(void) {
float f = 5.0;
int i = 2;
printf("%f\n",f/i); // Ergebnis = 2.500000
return 0;
}Die Ausgabe des Programms ist »2.500000«, weil der genauere der beiden Datentypen hier vom Typ float ist.
5.8.1 Gleitpunkttypen im Detail 

Bei Gleitpunkttypen wird auch von Zahlen mit gebrochenem Anteil (reellen Zahlen) gesprochen. Der C-Standard schreibt hierbei nicht vor, wie die interne Darstellung von reellen Gleitpunktzahlen erfolgen muss. Dies hängt von den Entwicklern der Compiler ab. Meistens wird aber der IEEE-Standard 754 verwendet (IEEE – Institute of Electrical and Electronics Engineers). In der Regel kann es dem Programmierer egal sein, wie Gleitpunktzahlen auf seinem System dargestellt werden. Trotzdem folgt hier für den interessierten Programmierer eine kurze Erklärung der internen Darstellung von Gleitpunktzahlen, ohne dass wir uns zu sehr in den Details verlieren wollen.
Gleitpunktzahlen werden halb logarithmisch dargestellt. Das heißt, die Darstellung einer reellen Gleitpunktzahl basiert auf einer Zerteilung in ein Vorzeichen, eine Mantisse und einen Exponenten zur Basis 2. Für echte Mathematiker sei gesagt, dass der Begriff »Mantisse« hier nichts mit einer Mantisse eines Logarithmus gemeinsam hat.
Die Genauigkeit nach dem Komma der Gleitpunktzahl hängt von der Anzahl der Bits ab, die der entsprechende reelle Datentyp in seiner Mantisse speichern kann. Der Wertebereich hingegen wird durch die Anzahl der Bits für den Exponenten festgelegt.
Hierzu folgen die Speicherbelegungen der einzelnen reellen Gleitpunktzahlen im IEEE-Format.
5.8.2 »float« im Detail 

float ist eine 32-Bit-Zahl. Diese 32 Bit teilen sich folgendermaßen auf:
Abbildung 5.2 »float« im Detail
- Vorzeichen-(Vz-)Bit (1 Bit): In Bit 31 wird das Vorzeichen der Zahl gespeichert. Ist dieses 0, dann ist die Zahl positiv, bei 1 ist sie negativ.
- Exponent (8 Bits): In Bit 23 bis 30 wird der Exponent mit einer Verschiebung (Bias) der Zahl gespeichert (Bias bei float 127).
- Mantisse (23 Bits): In Bit 0 bis 22 wird der Bruchteil der Mantisse gespeichert. Das erste Bit der Mantisse ist immer 1 und wird nicht gespeichert.
5.8.3 »double« im Detail 

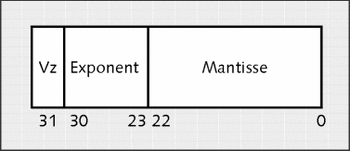
Beim Datentyp double ist es ähnlich wie bei float. double ist eine 64-Bit-Zahl mit doppelter Genauigkeit. double ist folgendermaßen aufgeteilt:
Abbildung 5.3 »double« im Detail
- Vorzeichen-Bit (1 Bit): In Bit 63 wird das Vorzeichen der Zahl gespeichert. Ist dieses 0, dann ist die Zahl positiv, bei 1 ist sie negativ.
- Exponent (11 Bit): In Bit 52 bis 62 wird der Exponent mit einer Verschiebung (Bias) der Zahl gespeichert (Bias bei double 1023).
- Mantisse (52 Bit): In Bit 0 bis 51 wird der Bruchteil der Mantisse gespeichert. Das erste Bit der Mantisse ist immer 1 und wird nicht gespeichert.
5.8.4 long double 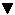

Wird dem Datentyp double das Schlüsselwort long vorangestellt, erhalten Sie eine 80-Bit-Zahl mit einer noch höheren Genauigkeit.
Wenn Sie long double mit dem sizeof-Operator auf seine Speichergröße in Bytes überprüft haben, dürften Sie sicherlich verwundert sein, dass der Datentyp auf 32-Bit-Systemen 12 Bytes beansprucht. Auf einem 32-Bit-System werden dazu einfach zwei Füllbytes angefügt. Auf 16-Bit-Systemen beansprucht long double weiterhin 10 Bytes Speicher. Auf einer HP-UX-Maschine hingegen benötigt long double gar 16 Bytes an Speicher. Dabei werden aber alle 128 Bits genutzt, und somit lässt sich eine Genauigkeit von 33 Stellen anzeigen.
| Internes |
|
Sollten Sie jetzt denken, mit long double erhielten Sie eine größere Genauigkeit, kann der Schein trügen. Intern (in der FPU) werden sowieso alle Werte, ob float oder double, erst nach long double konvertiert, und dann entsprechend zurück. Daher sollten Sie sich erst noch zwei Fälle durch den Kopf gehen lassen:
|
5.8.5 Einiges zu n-stelliger Genauigkeit 

Eine Fließkommazahl mit 6-stelliger Genauigkeit wie float kann sechs Dezimalstellen nicht immer korrekt unterscheiden. Wenn beispielsweise die Zahl vor dem Komma (z. B. »1234,1234«) bereits vier Stellen besitzt, so kann sie nach dem Komma nur noch zwei Stellen unterscheiden. Somit wären die Gleitpunktzahlen 1234,12345 und 1234,123999 als float-Zahlen für den Computer nicht voneinander zu unterscheiden. Mit 6-stelliger Genauigkeit sind die signifikanten Stellen von links nach rechts gemeint. Der Typ float ist also ungeeignet für kaufmännische und genaue wissenschaftliche Berechnungen. Dazu folgendes Beispiel:
/* floating.c */
#include <stdio.h>
int main(void) {
float x=1.1234;
float dollar=100000.12;
float end_float;
double y=1.1234;
double DOLLAR=100000.12;
double end_double;
printf("%f Euro mit float\n",end_float=dollar*x);
printf("%f Euro mit double\n",end_double=DOLLAR*y);
return 0;
}Hier werden zwei verschiedene Ergebnisse zurückgegeben. Die Differenz mag minimal sein, doch bei Börsenberechnungen könnte eine solche Ungenauigkeit durchaus Millionen von Euro kosten, und in der Astronomie wäre der Mond wohl heute noch nicht erreicht.
Abbildung 5.4 Darstellung von Fließkommazahlen mit »double« und »float«
float ist nach sechs Dezimalstellen am Ende. Mit double haben Sie dagegen die Möglichkeit, eine auf 15 Stellen genaue Zahl zu erhalten, und mit long double bekommen Sie eine 19-stellige.
Was ist zu tun, wenn diese Genauigkeit nicht ausreichen sollte? In diesem Fall müssen Sie sich nach sogenannten Festkomma-Algorithmen umsehen. Denn Festkomma-Darstellungen wie die BCD-Arithmetik gibt es in C nicht.
| BCD-Arithmetik |
|
BCD steht für Binary Coded Decimals und bedeutet, dass die Zahlen nicht binär, sondern als Zeichen gespeichert werden. Beispielsweise wird der Wert 56 nicht wie gewöhnlich als Bitfolge 00111000 gespeichert, sondern als die Werte der Ziffern im jeweiligen Zeichensatz. In unserem Fall wäre das im ASCII-Code-Zeichensatz. Und dabei hat das Zeichen »5« den Wert 53 und das Zeichen »6« den Wert 54. Somit ergibt sich dadurch folgende Bitstellung: 00110101 (53) 00110110 (54). Damit benötigt der Wert 53 allerdings 16 anstatt der möglichen 8 Bit. Für die Zahl 12345 hingegen benötigen Sie schon 40 Bits. Es wird zwar erheblich mehr Speicherplatz verwendet, doch wenn Sie nur die Grundrechenarten für eine Ziffer implementieren, können Sie mit dieser Methode im Prinzip unendlich lange Zahlen bearbeiten. Es gibt keinen Genauigkeitsverlust. |
| Hinweis |
|
Bei dem Listing oben wurde bei der formatierten Ausgabe für den Datentyp double %f verwendet, was übrigens bei der Ausgabe mit printf() nicht falsch ist. Verwenden Sie hingegen scanf(), kommt es zu Problemen. scanf() benötigt für double nämlich %lf. Dies liegt daran, dass Argumente in variablen Argumentlisten in C der Default Promotion unterliegen. Das heißt in diesem Fall, dass der Compiler versucht, einen Ausdruck vom Typ float in einen Ausdruck vom Typ double zu konvertieren. |
Ihre Meinung
Wie hat Ihnen das Openbook gefallen? Wir freuen uns immer über Ihre Rückmeldung. Schreiben Sie uns gerne Ihr Feedback als E-Mail an kommunikation@rheinwerk-verlag.de.





 Jetzt bestellen
Jetzt bestellen



