Das, wobei unsere Berechnungen versagen, nennen wir Zufall. – Albert Einstein

Kapitel 6 Zufall

Wenn Sie den Zufallsbegriff streng mathematisch auslegen, ist ein Computer gar nicht in der Lage, einen »Zufall« zu produzieren. Der Grund liegt auf der Hand: Ein Computer kann keine Zufallszahl aus irgendwelchen (tatsächlichen) Stromschwankungen ermitteln, sondern muss diese auf Basis eines Algorithmus berechnen.

Dennoch ist ein Computer in der Lage, relativ zufällige Zahlenfolgen zu produzieren. Es gibt eine Reihe von Methoden, um zufällige Zahlenfolgen zu bestimmen. Das Problem bei solchen Methoden ist jedoch immer der Startwert.

Wir stellen in diesem Kapitel einige Möglichkeiten vor, wie Sie selbst Zufallszahlen erzeugen können. Als Nächstes programmieren wir einige Hilfsfunktionen, die Ihnen einen schnellen Zugriff auf die Zufallszahlen ermöglichen. Am Ende des Kapitels zeigen wir noch einige Beispielapplikationen, die mit Zufallszahlen (und JavaScript) erstellt werden können.

Fast die komplette benötigte Funktionalität steckt in dem Math-Objekt von JavaScript, unter anderem die Ermittlung einer Zufallszahl und das Runden von Zahlen.

6.1 Zufallszahlen erstellen 

Bei der Ermittlung einer Zufallszahl haben Sie die freie Auswahl: Entweder Sie bedienen sich bei den mitgelieferten Funktionalitäten, oder Sie programmieren Ihren eigenen Zufallsgenerator.

6.1.1 JavaScript-Zufallszahlen 

Seit den Anfängen von JavaScript gibt es die Methode Math.random(), die eine (ziemlich) zufällige Zahl zwischen 0 und 1 zurückliefert. Die Browser bedienen sich hierbei eines internen Algorithmus. Als Startwert für diesen Algorithmus verwenden die Browser veränderliche Daten wie beispielsweise die aktuelle Uhrzeit sowie (bei manchen Algorithmen) benutzerspezifische Daten wie etwa den freien Speicher auf der Festplatte oder die MAC-Adresse der Netzwerkkarte.

Es ist nicht weiter schlimm, dass Math.random() eine Fließkommazahl zwischen 0 und 1 zurückliefert. Wenn Sie eine ganzzahlige Zufallszahl innerhalb eines bestimmten Bereichs haben möchten, können Sie aus der Fließkommazahl eine ganze Zahl ermitteln, behalten dabei aber das Zufallsmoment bei (mehr dazu später im Kapitel).

6.1.2 HP-Verfahren 

Das HP-Verfahren ist nach der amerikanischen Firma Hewlett-Packard benannt, die vor allem für ihre Tintenstrahl- und Laserdrucker bekannt ist. Die Entwicklungsabteilung der Firma hat der Legende nach den Algorithmus entwickelt (sie empfiehlt ihn zumindest vehement und baut ihn angeblich auch in die eigenen Produkte ein).

Der Algorithmus funktioniert folgendermaßen¹  :

Man beginne mit einer Zahl zwischen 0 und 1.

Man addiere zu dieser Zahl die Kreiszahl p (etwa 3,14159265...).

Das Ergebnis potenziere man mit 8 (umgangssprachlich: Das Ergebnis »hoch 8« nehmen).

Der Nachkommaanteil des Ergebnisses ist die nächste Zufallszahl.

Mit dem Nachkommateil starte man den Algorithmus erneut, um eine weitere Zufallszahl zu erhalten.

Es ist mathematisch nachgewiesen, dass dieser Algorithmus die (mathematischen) Bedingungen für einen Zufallsgenerator erfüllt; die entstehende Zahlenfolge ist tatsächlich zufällig.

Was uns fehlt, ist ein Startwert zwischen 0 und 1. Mit Math.random() ließe sich einer bestimmen, aber das würde die Grundidee unseres Vorgehens konterkarieren. Stattdessen setzen wir hier eine andere, weitere Methode zur Bestimmung einer Zufallszahl ein – auch wenn die nicht ganz so geeignet ist wie beispielsweise Math.random().

Mit dem Date-Objekt aus dem vorherigen Kapitel können Sie auf das aktuelle Datum und die aktuelle Uhrzeit zugreifen. Die Methode getTime() liefert die so genannte Epochenzeit zurück. Das ist die Anzahl der seit dem 1. Januar 1970, Mitternacht, verstrichenen Millisekunden.

Diese Zahl ist mehr oder wenig zufällig und damit ein besonders geeigneter Zufallswert für unsere Zwecke. Werfen wir einen Blick auf einen dieser Datumswerte: Rufen Sie dazu in Ihrem Browser die Pseudo-URL javascript:alert(new Date().getTime()) auf.

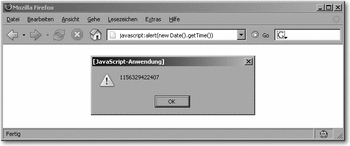
Hier klicken, um das Bild zu Vergrößern

Abbildung 6.1     Das ist tatsächlich eine Uhrzeit.

Als Startwert benötigen Sie aber eine Zahl zwischen 0 und 1. Aus diesem Grund müssen Sie vor die lange Zahl »0.« schreiben, um diese möglichst schnell in eine Fließkommazahl umzuwandeln.

Bevor der Zeitwert in eine Fließkommazahl umgewandelt wird, ist noch eine weitere Überlegung erforderlich. Wenn Sie die Zufallszahlengenerierung mehrmals hintereinander aufrufen, ähneln sich die ersten Zufallszahlen sehr, denn der Startwert ändert sich dort erst circa in der achten Nachkommastelle. Aus diesem Grund ist es eine gute Idee, das Ergebnis von getTime() umzudrehen, also die letzte Ziffer als erste Nachkommastelle zu verwenden, die vorletzte Ziffer als zweite Nachkommastelle und so weiter. Da viele Browser als letzte Ziffer von getTime()immer »0« liefern, ignorieren wir die letzte Ziffer vollständig.

var t = new Date().getTime();
var t2 = "";
for (var i=2; i<=t.length; i++) {
   t2 += t.charAt(t.length-i);
}
eval("var z = 0." + t2);

Am Ende enthält die Variable z eine (recht zufällige) Zahl zwischen 0 und 1.

Nun kann der Rest des Algorithmus programmiert werden: Zur Zahl wird p hinzuaddiert (p steht bei JavaScript in der Eigenschaft Math.PI zur Verfügung):

z += Math.PI;

Dann wird das Ergebnis mit 8 potenziert – mit der Methode pow() des Math-Objekts:

z = Math.pow(z, 8);

Die neue Zufallszahl ist dann der Nachkommaanteil des Ergebnisses – das ermitteln Sie mit der Methode floor() des Math-Objekts:

z -= Math.floor(z);

Das Gegenstück zu floor() ist die Methode ceil() – die rundet nämlich ab.

Die folgende Funktion fasst dieses Vorgehen zusammen. Die jeweils letzte Zufallszahl wird in einer globalen Variablen gespeichert, damit sie beim nächsten Aufruf der Funktion wieder als Startwert verwendet werden kann.

var zufall_hp_zahl = 0;
function zufall_hp() {
   if (zufall_hp_zahl == 0) {
      var t = new Date().getTime().toString();
      var t2 = "";
      for (var i=2; i<=t.length; i++) {
         t2 += t.charAt(t.length-i);
      }
      eval("zufall_hp_zahl = 0." + t2 + ";");
   }
   zufall_hp_zahl += Math.PI;
   zufall_hp_zahl = Math.pow(zufall_hp_zahl, 8);
   zufall_hp_zahl -= Math.floor(zufall_hp_zahl);
   return zufall_hp_zahl;
}

6.1.3 Datumswert 

Betrachten Sie noch einmal, was der Browser bei der Eingabe der Pseudo-URL javascript:alert(new Date().getTime()) ausgibt (siehe auch Abbildung 6.1). Sie erhalten eine recht lange Zahl, die offensichtlich immer auf 0 endet. Das hat mit den browserinternen Abläufen zu tun sowie mit der Unfähigkeit, auf die Millisekunde genau zu messen. Für Sie entscheidend ist aber, dass Sie diesen Wert durch 10 teilen sollten, um eine »zufälligere« Zahl zu erhalten:

var z = new Date().getTime();
z = Math.round(z / 10);

Wenn Sie nun eine ganzzahlige Zufallszahl benötigen, gibt es eine einfache Möglichkeit, diese zu ermitteln. Verwenden Sie die Modulo-Rechnung!

Unter Modulo versteht man den Rest, den eine Division liefert. Unter JavaScript ist der Modulo-Operator %. 15  % 7 liefert als Ergebnis 1, denn bei der Division von 15 durch 7 bleibt als Rest 1 übrig (15 = 2 × 7 + 1).

Ein wenig mathematischer: Der Rest bei einer Division durch N ist eine Zahl zwischen 0 und N-1. Wenn Sie also eine Zufallszahl zwischen 0 und N haben möchten, können Sie wie folgt vorgehen:

var z = new Date().getTime();
z = Math.round(z / 10);
z %= n;

Die folgende Funktion setzt dieses Vorgehen allgemein für die Aufgabenstellung »berechne eine Zufallszahl zwischen a und b« um.

function zufall_datum(a, b) {
   var spanne = b – a + 1; // Länge des Intervalls
   var z = new Date().getTime();
   z = Math.round(z / 10);
   z %= spanne;  // z ist zwischen 0 und spanne-1
   z += a; // z ist nun zwischen a und b
   return z;
}