21.4 Queues nach dem FIFO-Prinzip

Eine weitere Art der abstrakten Datenstrukturen sind Queues (dt.: Warteschlangen). Queues können Sie sich vorstellen wie eine Warteschlange an der Einkaufskasse. Der Kunde, der sich als Erster angestellt hat, kommt auch als Erster dran. Alle anderen Kunden müssen sich immer hinten anstellen und warten, bis sie an der Reihe sind (sollten sie zumindest).

Die Operationen einer Queue (Element hineinschieben und Element herausholen) werden Put und Get genannt. Im Gegensatz zum Stack erscheinen die Elemente in der gleichen Reihenfolge, in der sie hineingesteckt wurden. Eine Queue wird deshalb auch First-in-First-out-Datenstruktur (FIFO-Datenstruktur) genannt.

Als Modell einer Queue können Sie sich ein Rohr vorstellen, das an beiden Enden offen ist. An einem Ende werden neue Elemente hineingeschoben, am anderen Ende werden sie wieder entnommen. Wie auch schon der Stack setzt sich die Queue aus zwei grundlegenden Funktionen zusammen:

• get() – ein neues Element wird am Ende der Queue angefügt.

• put() – ein Element wird am anderen Ende entnommen.

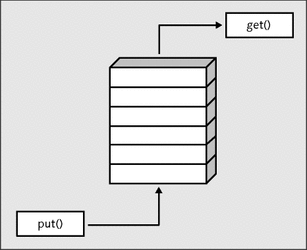
Abbildung 21.48 verdeutlicht das Prinzip einer Queue:

Abbildung 21.48 Eine Warteschlange und ihre Funktionen »get()« und »put()«

In der Praxis können Sie Queues recht vielseitig einsetzen. Eine interessante Lösung für das umfangreiche Listing, das Sie in Abschnitt 21.3 erstellt haben, wäre, das Speichern von Daten mithilfe einer Queue zu realisieren. Sinn macht dies vor allem bei einem System, bei dem mehrere User gleichzeitig auf Daten zugreifen müssen – insbesondere dann, wenn mehrere User versuchen, gleichzeitig in dieselbe Datei zu schreiben. Mit den Queues können Sie dabei sogenannte Deadlocks vermeiden.

Keine Sorge, ich werde das Thema hier nicht wieder auf das mittlerweile schon recht umfangreiche Listing ausweiten. Wenn Sie wollen, können Sie den Suchbegriff »Queues C« einmal in eine Suchmaschine eingeben. Sie werden dabei eine Menge Anwendungsbeispiele – auch betriebssystemspezifische – finden.

Ein Szenario: Damit ein Arzt sich einen Überblick darüber verschaffen kann, ob noch Patienten im Wartezimmer sind und vor allem welcher Patient als Nächstes an der Reihe ist, soll ein Programm geschrieben werden. Die Daten eines neuen Patienten werden von der Assistentin am Empfang eingegeben. Zuerst schreiben wir die Funktion zum Initialisieren einer Warteschlange:

int schlange_init(void) {
   if((dummy=
     malloc(sizeof(struct reservierung))) != NULL) {
      strcpy(dummy->name,"dummy");
      strcpy(dummy->vorname,"dummy");
      dummy->nummer=0;
      dummy->previous=NULL;
      return 1;
   }
   else {
      fprintf(stderr, "Konnte keinen Speicher "
                      "reservieren!!\n");
      return 0;
   }
}

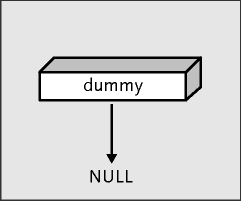
Auch hierzu wird als Kopf eine Art dummy verwendet. Dieser zeigt immer den Anfang der Warteschlange an. Zuerst wird ein Speicherplatz für dummy reserviert und anschließend mit sinnlosen Werten initialisiert. Der previous-Zeiger zeigt somit am Anfang wieder auf NULL:

Abbildung 21.49 Eine »leere« Warteschlange

Als Nächstes wird eine Funktion benötigt, die ein neues Element immer an das Ende der Warteschlange hängt:

int put(struct reservierung *neu) {
   struct reservierung *zeiger;

  /* Ist es das 1. Element in der Schlange? */
   if(dummy->previous == NULL) { /* Es ist das 1. Element. */
      dummy->previous=neu;
      neu->previous=NULL;
      return 1;
   }
   /* Es ist nicht das 1. Element. */
   else {
      zeiger=dummy;
      /* Wir suchen das Ende der Schlange */
      while(zeiger->previous != NULL)
         zeiger=zeiger->previous;
      zeiger->previous=neu;
      neu->previous=NULL;
      return 1;
   }
}

Zuerst wird überprüft, ob sich hinter dem Anfang der Warteschlange ein Element befindet. Das ist am Anfang nicht der Fall, und somit wird ein neues Element hinten angefügt:

dummy->previous=neu;

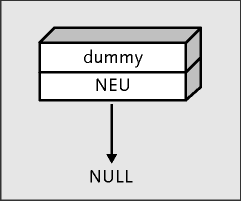
Das neue Element zeigt hinter sich momentan noch auf gar nichts. Hier sehen Sie den aktuellen Stand:

Abbildung 21.50 Ein neues Element wird hinten angefügt.

Falls dummy schon hinter sich auf ein Element zeigt, wird mit

zeiger=dummy;
while(zeiger->previous != NULL)
    zeiger=zeiger->previous;

die Warteschlange von vorn bis zum Ende durchlaufen, bis zeiger->previous auf das Ende der Warteschlange (NULL) verweist. Anschließend wird, wie schon das erste Element der Warteschlange, das neue Element hinten angehängt.

Als Nächstes wird noch eine Funktion benötigt, um das eingefügte Element in der Warteschlange wieder zu entfernen und das zweite Element in der Warteschlange zum ersten zu machen. Hier sehen Sie die Funktion dazu:

void get(void) {
   struct reservierung *zeiger;
   /* Ist überhaupt etwas in der Schlange? */
   if(dummy->previous != NULL) { /*Es ist...!*/
      zeiger=dummy->previous;
      dummy->previous=zeiger->previous;
      free(zeiger);
   }
   else
      fprintf(stderr,"Es sind keine Patienten "
                     "im Wartezimmer.....\n");
}

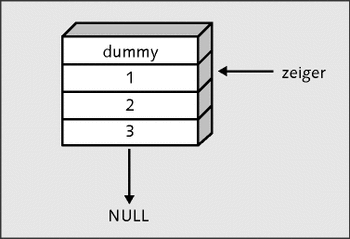
Zuerst wird überprüft, ob überhaupt ein Nachfolger von dummy vorhanden ist. Falls nicht, ist die Liste leer. Ist die Liste nicht leer, dann bekommt ein Zeiger die Adresse des ersten Elements in der Warteschlange:

zeiger=dummy->previous;

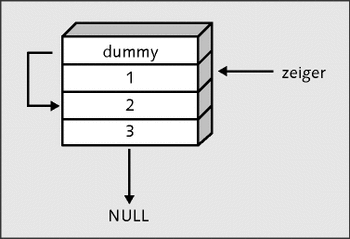
Abbildung 21.51 Das zuerst eingefügte Element entfernen

Bevor Sie das erste Element, auf das der Zeiger zeiger verweist, mit free(zeiger) freigeben können, muss noch eine Zeile Code eingefügt werden, damit das (noch) zweite Element zum ersten Element in der Warteschlange wird:

dummy->previous=zeiger->previous;

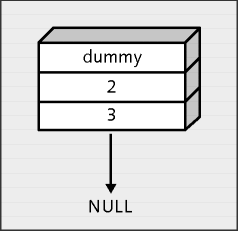
Abbildung 21.52 Das zuerst eingefügte Element »aushängen«

free(zeiger);

Abbildung 21.53 Speicherplatz des ersten Elements wurde freigegeben.

Dies sind alle Funktionen einer Warteschlange. Jetzt folgt das Demonstrationsprogramm, das diese Funktionen einsetzt und natürlich enorm erweiterbar ist:

/* queues.c */
#include <stdio.h>
#include <stdlib.h>
#include <string.h>
#define MAX 20

struct reservierung {
   char name[MAX];
   char vorname[MAX];
   int rnummer;
   struct reservierung *previous;
};

struct reservierung *dummy;
static int nummer = 1;

int schlange_init(void) {
   if((dummy=malloc(sizeof(struct reservierung))) != NULL)  {
      strcpy(dummy->name,"dummy");
      strcpy(dummy->vorname,"dummy");
      dummy->rnummer=0;
      dummy->previous=NULL;
      return 1;
   }
   else {
      fprintf(stderr,"Konnte keinen Speicher reservieren!!\n");
      return 0;
   }
}

/* Wir hängen ein neues Element an das Ende der Schlange. */
int put(struct reservierung *neu) {
   struct reservierung *zeiger;

   /* Ist es das 1. Element in der Schlange? */
   if(dummy->previous == NULL) { /* Es ist das 1. Element. */
      dummy->previous=neu;
      neu->previous=NULL;
      return 1;
   }
   /* Es ist nicht das 1. Element. */
   else {
      zeiger=dummy;
      /* Wir suchen das Ende der Schlange. */
      while(zeiger->previous != NULL)
         zeiger=zeiger->previous;
      zeiger->previous=neu;
      neu->previous=NULL;
      return 1;
   }
}

/* Wir benötigen das 1. Element der Liste, das wir auch als 1.
 * eingegeben haben. */
void get(void) {
   struct reservierung *zeiger;

   /* Ist überhaupt etwas in der Schlange? */
   if(dummy->previous != NULL) { /* Es ist...! */
      zeiger=dummy->previous;
      dummy->previous=zeiger->previous;
      free(zeiger);
   }
   else
      fprintf(stderr,"Es sind keine Patienten "
                     "im Wartezimmer.....\n");
}

void eingabe(void) {
   struct reservierung *neu;
   char n[MAX],vn[MAX];

   if((neu=(struct reservierung *)
     malloc(sizeof(struct reservierung))) != NULL) {
      printf("Name.....: ");
      fgets(n, MAX, stdin);
      strcpy(neu->name, strtok(n,"\n"));
      printf("Vorname..: ");
      fgets(vn, MAX, stdin);
      strcpy(neu->vorname,strtok(vn,"\n"));
      printf("Nummer...: ");
      printf("%d\n",neu->rnummer = nummer++);
      neu->previous=NULL;
      put(neu);
   }
}

void ausgabe(void) {
   if(dummy->previous != NULL) {
      printf("\n%s, %s Nummer.: %d \n\n",
      dummy->previous->name,dummy->previous->vorname,
      dummy->previous->rnummer);
      get();
   }
   else
      printf("Keine Patienten im Wartezimmer vorhanden!!!\n");
}

int main(void) {
   int wahl;

   schlange_init();
   do {
      printf("-1- Reservierung eingeben\n");
      printf("-2- Naechster Patient\n");
      printf("-3- Programmende\n\n");
      printf("Ihre Wahl : ");
      scanf("%d",&wahl);
      getchar();
      switch(wahl) {
         case 1  : eingabe();
                   break;
         case 2  : ausgabe();
                   break;
         case 3  : if(dummy->previous != NULL) {
                      printf("Es sind noch Patienten"
                             " im Wartezimmer!!!\n");
                      wahl = 4; /* Abhauen gilt nicht */
                   }
                   break;
         case 4  : break;
         default : printf("Falsche Eingabe!!\n\n");
      }
   } while(wahl != 3);
   printf("\n\nFeierabend\n");
   return EXIT_SUCCESS;
}

Hiermit ist der Abschnitt »Lineare Listen« erst einmal beendet. Später, in Kapitel 22, »Algorithmen«, wird dieses Wissen um den Bereich der binären Bäume erweitert.

Ihre Meinung

Wie hat Ihnen das Openbook gefallen? Wir freuen uns immer über Ihre Rückmeldung. Schreiben Sie uns gerne Ihr Feedback als E-Mail an kommunikation@rheinwerk-verlag.de.