11.2 Bögen und Trigonometrie 

Nun begegnen Sie einem Teilgebiet der Mathematik, das viele Schüler nicht besonders gerne mögen: der Geometrie. Bögen, Winkel, Sinus und Kosinus gibt es auch in ActionScript. Und dort haben sie einen großen praktischen Nutzen: Bewegungen lassen sich mit ihnen natürlicher, Animationen spannender gestalten.
Bevor Sie aber mit Sinus, Kosinus und Tangens arbeiten, erklären wir Ihnen im nächsten Abschnitt einige wichtige Begriffe, die wesentlich zum Grundverständnis beitragen. Anschließend zeigen wir Ihnen anhand eines einfachen Beispiels, wie Sie mit den trigonometrischen Methoden der Math-Klasse umgehen.
Trigonometrie – am Einheitskreis erklärt
Der Einheitskreis ist ein Kreis mit dem Radius 1. Daraus ergibt sich der Durchmesser von 2 und ein Umfang von 2 * . ist die schon erwähnte Kreiszahl mit dem ungefähren Wert 3,14; sie ist als Math.PI auch in der Liste aller Konstanten der Math-Klasse enthalten.
Legen Sie ein Koordinatensystem durch den Einheitskreis, erhalten Sie zwei Achsen: Die Horizontale x und die Vertikale y. Der Ursprung liegt beim Einheitskreis immer im Kreismittelpunkt. Wenn Sie nun einen Winkel zwischen den Achsen einzeichnen, beispielsweise 60°, hat die Länge der Gerade den Wert 1 vom Kreismittelpunkt bis zum Schnittpunkt mit dem Kreis.
Abbildung 11.2 Der Einheitskreis zeigt Sinus und Kosinus.
Die Gerade selbst ist in der Sprache der Dreiecke die Hypotenuse. Der Sinus ist der Wert aus der Gegenkathete geteilt durch die Hypotenuse. Da die Hypotenuse den Wert 1 hat, nimmt der Sinus im Einheitskreis den Wert der Gegenkathete an. Diese entspricht in unserem System der y-Achse. Der Sinus von 60° ist also 0,866. Der Kosinus ist definiert als Ankathete geteilt durch die Hypotenuse. Die Ankathete entspricht der y-Achse und besteht aus einem deutlich kürzeren Streckenabschnitt. Der Kosinus von 60° beträgt nur 0,5. Zum Schluss betrachten wir noch den Tangens im Einheitskreis. Er hat den Wert Gegenkathete geteilt durch die Ankathete. Der Tangens von 60° ist also 0,866 / 0,5; das ergibt 1.732.
Wenn Sie sich spezielle Winkel einprägen, können Sie Sinus und Kosinus bei anderen Winkeln fast schon schätzen. Wichtige Beispiele sind: Bei einem Winkel von 0 ist der Sinus 0, die Gegenkathete existiert nicht, der Kosinus beträgt 1, die Hypotenuse liegt auf der Ankathete. Bei einem Winkel von 90° beträgt der Sinus 1, die Hypotenuse ist identisch mit der Gegenkathete, der Kosinus hat den Wert 0.
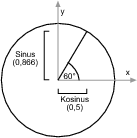
Das waren Sinus, Kosinus und Tangens im gewohnten Koordinatensystem. Wenn Sie das übliche Flash-Koordinatensystem mit Ursprung links oben zu Grunde legen, spiegelt sich die letzte Abbildung einfach in der nächsten. Ansonsten gibt es aber keine Unterschiede.
Abbildung 11.3 Der Einheitskreis mit dem typischen Flash- Koordinatensystem
| Rechenfehler |
|
Flash speichert die Konstanten wie beispielsweise PI nicht absolut exakt bzw. bis zu den aktuell wirklich bekannten Stellen. Dadurch werden die Rechenergebnisse, besonders bei den hinteren Stellen, etwas ungenau. Wenn Sie beispielsweise 90° in das Bogenmaß umwandeln und dann den Kosinus berechnen, erhalten Sie eine Zahl, die fast 0 ist, aber eben nicht genau 0. |
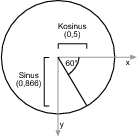
Oftmals wird auch die Wertentwicklung des Sinus oder Kosinus über verschiedene Winkel abgebildet. Daraus ergeben sich die berühmten Sinus- oder Kosinuskurven. Für die Animation ist dies durchaus wichtig, da Sinus und Kosinus eine wellenförmige Bewegung liefern können.
Abbildung 11.4 Der Verlauf des Sinus – die y-Achse zeigt den Wert, die x-Achse den Winkel.
Trigonometrie in ActionScript
ActionScript bietet für alle bekannten trigonometrischen Funktionen eine Methode des Math-Objekts: sin(Winkel) für den Sinus, cos(Winkel) für den Kosinus und tan(Winkel) für den Tangens. Der Winkel wird dabei jeweils im Bogenmaß angegeben.
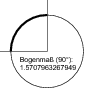
Die Umwandlung eines Winkels in das Bogenmaß ist sehr einfach: Das Bogenmaß ist die Länge des Kreisbogens, den der Winkel aus dem Einheitskreis herausschneidet. So wandeln Sie einen Winkel in ein Bogenmaß um:
var bm_num:Number = Math.PI * Winkel / 180;
Und so klappt die Rückverwandlung vom Bogenmaß in einen Winkel:
Abbildung 11.5 Das Bogenmaß ist die Länge des Kreisbogens, geschnitten aus dem Einheitskreis.
var w_num:Number = 180 * Bogenmaß / Math.PI;
Das folgende Beispiel zeigt, wie Sie den Sinus einsetzen können, um eine einfache Pendelbewegung zu realisieren.
Wichtig ist der Registrierungspunkt des MovieClips. Er bildet den Drehpunkt der Pendelbewegung.
Die Ausgangsdatei mit dem MovieClip ist schaukelstuhl.fla auf der CD-ROM im Ordner FlashMX2004 bzw. FlashMX.
Abbildung 11.6 Im Schaukelstuhl schläft es sich bequem.
Ziel ist, den Kopf und den Körper mit Schaukelstuhl in verschiedenen Geschwindigkeiten pendeln zu lassen.
Schritt für Schritt: Schaukelstuhl mit Pendelbewegung
Dieses Beispiel setzen Sie wieder komplett mit Ereignisprozeduren um. Der Code landet im ersten Schlüsselbild des Hauptfilms.
Zuerst definieren Sie eine Variable, die die Änderung aufnimmt:
var aenderung_num:Number = 0;
Die Änderung ist die Grundlage der Pendelbewegung.
Anschließend verwenden Sie onEnterFrame, um ein immer wiederkehrendes Ereignis zu realisieren. Das erste Ereignis ist für den MovieClip des Stuhls zuständig:
_root.stuhl_mc.onEnterFrame = function() {
_root.stuhl_mc._rotation = rotieren(1, 15);
};
Das zweite Ereignis dient für den Kopf:
_root.stuhl_mc.kopf_mc.onEnterFrame = function() {
_root.stuhl_mc.kopf_mc._rotation = rotieren(1, 20);
};Der Code in den zwei Ereignisprozeduren wird ständig ausgeführt – und zwar in der Bildrate (Geschwindigkeit) des gesamten Films.
In unserem Beispiel weist der Code dem MovieClip des Stuhls beziehungsweise des Kopfes einen neuen Rotationswinkel zu (Eigenschaft _rotation). Diesen Winkel berechnet die Funktion rotieren().
Sie erhält zwei Parameter: Wie schnell das Pendel sich bewegen soll und bis zu welchem Winkel es maximal ausschlägt. Übrigens, alternativ zu onEnterFrame können Sie auch setInterval() verwenden.
Die Bewegung führen Sie in der Funktion rotieren() durch. Dort berechnen Sie die Rotation und liefern sie zurück:
function rotieren(geschwindigkeit_num:Number,
ausschlag_num:Number):Number {
var rotation_num:Number = Math.sin(geschwindigkeit_
num * aenderung_num) * ausschlag_num;
aenderung_num += 0.1;
return rotation_num;
}Hier kommt der Sinus zum Einsatz, um die Rotation regelmäßig zu gestalten. Der Sinus erhält als Wert die Geschwindigkeit multipliziert mit der Änderung. Das heißt, der Sinuswert ist bei jedem Aufruf der Funktion anders, da die Änderung (aenderung_num) nach jedem Durchgang um 0,1 erhöht wird.
Der Sinus liefert Ergebnisse zwischen –1 (Pendelbewegung nach links) und +1 (Pendelbewegung nach rechts). Die Multiplikation dieser Ergebnisse mit dem maximalen Winkel ergibt den Rotationswinkel des MovieClips.
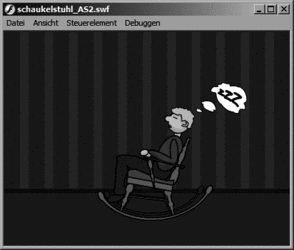
Abbildung 11.7 Kopf und Schaukelstuhl schaukeln in trauter Eintracht.
Die fertige Datei schaukelstuhl_AS2.fla finden Sie im Ordner Flash8 bzw. FlashMX2004. Die Flash MX-Variante heißt schaukelstuhl_AS1.fla und liegt im Ordner FlashMX.
Ihre Meinung
Wie hat Ihnen das Openbook gefallen? Wir freuen uns immer über Ihre Rückmeldung. Schreiben Sie uns gerne Ihr Feedback als E-Mail an kommunikation@rheinwerk-verlag.de.



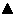




 bestellen
bestellen



